Fonctions logarithme 1 — Analytique

Définition

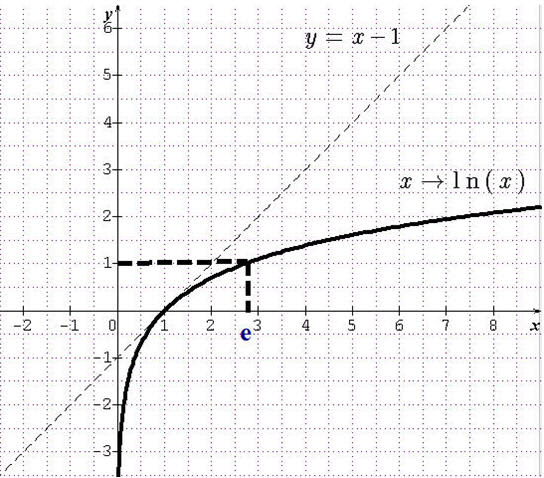
La fonction logarithme népérien définie sur $]0~;+\infty[$ est la fonction $x \mapsto \ln(x)$ où le nombre réel $\ln(x)$ est l'unique solution de l'équation $\mathrm e^{y} = x$ d'inconnue $y$.

Propriétés de base

Elle est définie, continue, dérivable sur l'intervalle $]0~ ;+\infty[$. Pour tout $x \in\:]0~ ;+\infty[$, $\displaystyle \ln'(x) = \frac{1}{x} > 0$ donc la fonction $\ln$ est strictement croissante sur l'intervalle $]0 ~;+\infty[$.

$\ln(1) = 0$ et $\ln x < 0$ pour $x \in \:]0~ ;1[$ et $\ln x > 0$ pour $x \in \:]1~ ;+\infty[$ car la fonction $\ln$ est strictement croissante sur l'intervalle $]0~ ;+\infty[$.

Propriétés

Pour tous les réels $a$ et $b$ strictement positifs :

Propriétés algébriques du logarithme

• $\ln(a \times b) = \ln(a) + \ln(b)$
• $\displaystyle \ln\left(\frac{1}{b}\right) = -\ln(b)$
• $\displaystyle \ln\left(\frac{a}{b}\right) = \ln(a) - \ln(b)$
• $\ln({a}^{n}) = n \ln(a)$ ($n$ entier naturel)
• $\displaystyle \frac{1}{2} \ln(a) = \ln(\sqrt{a})$

Dérivée de $\ln(u)$

Pour une fonction $u$ strictement positive et dérivable sur un intervalle $\rm I$, $\ln(u)$ est dérivable sur $\rm I$ et :

$\displaystyle (\ln(u))' = \frac{u'}{u}$ sur cet intervalle.

Limites

Limite en $0^+$

La limite de la fonction logarithme népérien quand $x$ tend vers $0$ par valeurs positives est :

$$\lim_{x \to 0^+} \ln(x) = - \infty$$

Limite en $+ \infty$

La limite de la fonction logarithme népérien quand $x$ tend vers $+ \infty$ est :

$$\lim_{x \to + \infty} \ln(x) = + \infty$$

On en déduit l'existence d'une asymptote verticale d'équation $x = 0$.

Croissances comparées de fonctions

Pour tout entier naturel non nul $n$, nous avons les propriétés suivantes :

$$\lim_{x \to + \infty} \frac{\ln(x)}{x^n} = 0^+$$

$$\lim_{x \to 0^+} x^n \ln(x) = 0$$

Ainsi, la fonction $x \mapsto x^n$ l'emporte sur la fonction logarithme népérien en $0^+$ et $+\infty$, pour tout entier naturel $n$ non nul.

Représentation graphique

La représentation graphique de la fonction logarithme népérien illustre ses propriétés de limites et son comportement asymptotique.

Propriétés de la fonction logarithme népérien

La fonction logarithme népérien est continue et strictement croissante, donc pour tous les nombres réels strictement positifs $a$ et $b$ :

Équivalences importantes

• Égalité : $\ln(a) = \ln(b) \Leftrightarrow a = b$
• Inégalité stricte (inférieur) : $\ln(a) < \ln(b) \Leftrightarrow a < b$
• Inégalité stricte (supérieur) : $\ln(a) > \ln(b) \Leftrightarrow a > b$

La fonction logarithme décimal

La fonction logarithme décimal, notée $\log$, est la fonction définie sur ${\mathbb{R}}_+^*$ par :

$$\log(x) = \frac{\ln(x)}{\ln(10)}$$

Propriétés algébriques

La fonction $\log$ possède les mêmes propriétés algébriques que la fonction logarithme népérien :

• $\log(1) = 0$
• $\log(10) = 1$
• $\log(10^{n}) = n \log (10) = n$ pour tout $n \in \mathbb{N}$

Applications

La fonction $\log$ est fréquemment utilisée en physique, en chimie et en acoustique.