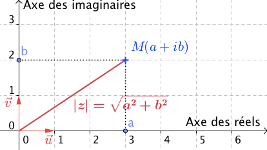Nombres complexes

1. Théorème admis, définition et propriétés

Il existe un ensemble noté $\mathbb{C}$, appelé ensemble des nombres complexes qui contient $\mathbb{R}$ et qui vérifie les propriétés suivantes :

1. $\mathbb{C}$ est muni d'une addition (notée $+$) et d'une multiplication (notée $\times$) qui ont les mêmes propriétés que les opérations analogues dans $\mathbb{R}$ et qui prolongent celles de $\mathbb{R}$.
2. $\mathbb{C}$ possède un élément $i$ tel que $i^2=-1$.
3. Tout nombre complexe $z$ s'écrit d'une manière unique sous la forme $z=a+i b$ avec $a \in \mathbb{R}$ et $b \in \mathbb{R}$. $a$ est appelé partie réelle du nombre complexe $z$. On note $a=\mathrm{Re}(z)$. $b$ est appelé partie imaginaire du nombre complexe $z$. On note $b=\operatorname{Im}(z)$.

L'écriture $a+i b$ est l'écriture algébrique (ou cartésienne) du nombre complexe $z$.

Remarque : La partie réelle et la partie imaginaire d'un nombre complexe sont des nombres réels.

Conséquence

1. On peut définir la soustraction et la division dans $\mathbb{C}$ par :
   $\forall\left(z_1, z_2\right) \in \mathbb{C}^2$, $z_1-z_2=z_1+\left(-z_2\right)$
   $\forall\left(z_1, z_2\right) \in \mathbb{C} \times \mathbb{C}^*$, $\dfrac{z_1}{z_2}=z_1 \times \dfrac{1}{z_2}$
2. La règle du produit nul reste valable dans $\mathbb{C}$ :
   $\forall\left(z_1, z_2\right) \in \mathbb{C}^2$, $z_1 \times z_2=0$ $\Rightarrow z_1=0 \text { ou } z_2=0$
3. Toutes les formules de calcul algébrique (notamment les identités remarquables, la formule du binôme, les formules relatives aux suites arithmétiques et géométriques, etc.) restent valables dans $\mathbb{C}$.
4. Règles de calcul :
   $$(a+i b)+\left(a^{\prime}+i b^{\prime}\right)\\=\left(a+a^{\prime}\right)+i\left(b+b^{\prime}\right)$$
   $$(a+i b) \times\left(a^{\prime}+i b^{\prime}\right)=\left(a a^{\prime}-b b^{\prime}\right)+i\left(a b^{\prime}+b a^{\prime}\right)$$
   En particulier : $(a+i b) \times(a-i b)=a^2+b^2$.
   Si $z=a+i b$ est un nombre complexe non nul, alors on a : $\dfrac{1}{z}=\dfrac{a}{a^2+b^2}+i \dfrac{-b}{a^2+b^2}$
5. Un nombre complexe est nul si et seulement si sa partie réelle et sa partie imaginaire sont nulles.
   $$a+i b=0 \Leftrightarrow a=0 \text { et } b=0$$

On en déduit que : Deux nombres complexes sont égaux si et seulement s'ils ont même partie réelle et même partie imaginaire :

$a+i b=a^{\prime}+i b^{\prime} \Leftrightarrow a=a^{\prime}$ et $b=b^{\prime}$

2. Représentation géométrique d’un nombre complexe

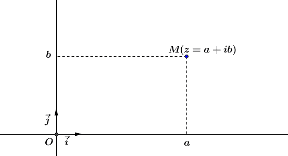
Le plan $\mathscr{P}$ orienté étant muni d'un repère orthonormé $(\mathrm O, \vec{\imath}, \vec{\jmath})$, à tout nombre complexe $z=a+i b$, on peut associer le point $\mathrm M(a, b)$ et inversement à tout point $\mathrm M$ défini par ses coordonnées dans ce repère, correspond un unique nombre complexe $z$ dont la partie réelle est l'abscisse de $\mathrm M$ et la partie imaginaire est l'ordonnée de $\mathrm M$.
$\mathscr P$ est alors appelé plan complexe. On dit que $\mathrm M$ est le point-image de $z$ et que $z$ est l'affixe du point $\mathrm M$.
(« Affixe » est un nom féminin). On note souvent $z_{\mathrm M}$ l'affixe du point $\mathrm M$.

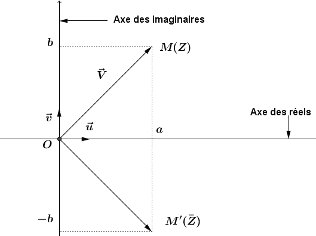
$\mathrm M$ est sur l'axe $(\mathrm O, \vec{u})$ (axe des réels) si et seulement si $z \in \mathbb{R}$.
$\mathrm M$ est sur l'axe $(\mathrm O, \vec{v})$ (axe des imaginaires purs) si et seulement si $z \in i \mathbb{R}$.
Soit $\overrightarrow{\mathrm V}=a \vec{u}+ b \vec{v}$ un vecteur quelconque.

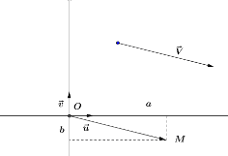
Il existe un unique point $\mathrm M$ tel que $\overrightarrow{\mathrm{OM}} = \overrightarrow{\mathrm V}$. L'affixe $z_{\mathrm M}$ de ce point $\mathrm M$ est, par définition, l'affixe du vecteur $\overrightarrow{\mathrm V}$. On note $z_{\overrightarrow{\mathrm V}}$ l'affixe du vecteur $\overrightarrow{\mathrm V}$. $\overrightarrow{\mathrm V}$ s'appelle le vecteur image du nombre complexe $z_{\mathrm M}$.

Propriétés :

1. Si $\mathrm A$ et $\mathrm B$ sont deux points du plan complexe d'affixes respectives $z_{\mathrm A}$ et $z_{\mathrm B}$, alors le vecteur $\overrightarrow{\mathrm{A B}}$ a pour affixe $z_{\mathrm B}-z_{\mathrm A}$ et le milieu $\mathrm I$ de $\rm [A B]$ a pour affixe $\dfrac{z_{\mathrm A} + z_{\mathrm B}}{2}$.
2. Quels que soient les vecteurs $\overrightarrow{\mathrm U}$ et $\overrightarrow{\mathrm V}$ et le réel $\lambda$, on a :
   $$z_{\overrightarrow{\mathrm{U}}+\overrightarrow{\mathrm {V}}}=z_{\overrightarrow{\mathrm{U}}}+z_{\overrightarrow{\mathrm{V}}} \text { et } z_{\overrightarrow{\lambda\mathrm V}}=\lambda z_{\overrightarrow{\mathrm{V}}}$$
3. Si $\mathrm A$ et $\mathrm B$ sont deux points du plan complexe et $\alpha$ et $\beta$ deux réels tels que $\alpha+\beta \neq 0$, alors l'affixe du barycentre $\mathrm G$ des points pondérés $(\mathrm A, \alpha)$ et $(\mathrm B, \beta)$ $(\alpha+\beta \neq 0)$ est : $\dfrac{\alpha z_A+\beta z_{\mathrm B}}{\alpha+\beta}$.

De manière analogue, on peut étendre cette formule au barycentre de 3, ou 4 points pondérés. Pour un système de 3 points $(\mathrm A, \alpha)$, $(\mathrm B, \beta)$ et $(\mathrm C, \gamma)$ par exemple, on a pour l'affixe de $\mathrm G$ :

$z_{\mathrm{G}}=\dfrac{\alpha z_{\mathrm A}+\beta z_{\mathrm B}+\gamma z_{\mathrm C}}{\alpha+\beta+\gamma}$

Les propriétés précédentes permettent de traduire des problèmes de géométrie en relations entre nombres complexes. Par exemple, la combinaison linéaire de deux vecteurs sera traduite par la combinaison linéaire de leurs affixes, l'égalité de deux vecteurs sera traduite par l'égalité de leurs affixes, etc.

1. Définition

Soit $z$ un nombre complexe de la forme algébrique $a+i b$. Le nombre complexe de la forme algébrique $a- ib$ est appelé conjugué du nombre complexe $z$ et noté $\overline{Z}$.

Remarque : On a aussi $\overline{\mathrm{Z}}=z$. On dit que $\mathrm Z$ et $\overline{\mathrm{Z}}$ sont des nombres complexes conjugués.

Exemples :

• $\overline{9-4 \imath}=9+4 i$ ;
• $\bar{\imath}=\overline{0+1 \imath}=0-1 i=-i$ ;
• $\overline{7}=7$

2. Interprétation géométrique

Dans le plan complexe muni d'un repère orthonormé, les images de deux nombres complexes conjugués sont symétriques par rapport à l'axe des réels : $\mathrm{M}^{\prime}(\bar{z})=\mathrm{S}_{(0, \vec{u})}(\mathrm{M}(z))$

3. Propriétés

1. $\forall z \in \mathbb{C}: \operatorname{Re}(z)=\operatorname{Re}(\overline{z})$ et $\operatorname{Im}(\overline{z})=-\operatorname{Im}(z)$.
2. $\forall\left(z, z^{\prime}\right) \in \mathbb{C}^2, \overline{z+z^{\prime}}=\bar{z}+\overline{z^{\prime}}$
3. $\forall\left(z, z^{\prime}\right) \in \mathbb{C}^2, \overline{z z^{\prime}}=\bar{z} \times \overline{z^{\prime}}$
4. $\forall z \in \mathbb{C}^*$ : $\overline{\left(\dfrac{1}{z}\right)}=\dfrac{1}{\bar{z}}$
5. $\forall \lambda \in \mathbb{R}$, $\forall z \in \mathbb{C}$, $\overline{\lambda z}=\lambda \bar{z}$.
6. $\forall z \in \mathbb{C}$, $\forall n \in \mathbb{Z}$, $\overline{z^n}=\bar{z}^n$
7. $\forall\left(z, z^{\prime}\right) \in \mathbb{C} \times \mathbb{C}^*$ : $\overline{\left(\dfrac{z}{z^{\prime}}\right)}=\dfrac{\bar{z}}{\overline{z^{\prime}}}$
8. $\forall z \in \mathbb{C}$ : $z+\bar{z}=2 \operatorname{Re}(z)$ ou encore $\operatorname{Re}(z)=\dfrac{z+\bar z}{2}$
9. $\forall z \in \mathbb{C}$ : $z-\bar{z}=2 i \operatorname{Im}(z)$ ou encore $\operatorname{Im}(z)=\dfrac{z-\bar z}{2 i}$
10. $\forall z \in \mathbb{C}$, si $z$ de forme algébrique $a+i b$, alors $z \bar{z}=a^2+b^2$, donc $z \bar{z}$ est un réel positif.
11. $z$ est réel si et seulement si $z=\bar{z}$.
12. $z$ est imaginaire si et seulement si $z=-\bar{z}$.

1. Définition

Le module du nombre complexe de forme algébrique $z=a+i b$ est le réel positif noté

$|z|=\sqrt{a^2+b^2}$

Exemples : $|2-\sqrt{3} i|=\sqrt{2^2+(-\sqrt{3})^2}=\sqrt{7} ;|i|=1 ;|-3|=3$.

2. Interprétation géométrique

Soit $\mathrm M(z=a+i b)$ dans le plan complexe muni d'un repère orthonormé $(\mathrm O, \vec{u}, \vec{v})$.

Alors $|z|=\mathrm{OM}=\sqrt{a^2+b^2}$.

3. Propriétés

1. $\forall z \in \mathbb{C}$ : $|\bar{z}|=|-z|=|-\bar{z}|=|z|$
2. Soient $\rm A$ et $\rm B$ deux points du plan complexes d'affixes respectives $z_{\mathrm A}$ et $z_{\mathrm B}$. Alors, la distance $\rm AB$ est égale à $\left|z_{\mathrm B}-z_{\mathrm A}\right|$.
3. $\forall z \in \mathbb{C}$ : $z \bar{z}=|z|^2$
4. $\forall z \in \mathbb{C}$ : $\operatorname{Re}(z) \leq|z|$ et $\operatorname{Im}(z) \leq|z|$.
5. $\forall\left(z, z^{\prime}\right) \in \mathbb{C}^2$, $\left|z z^{\prime}\right|=|z| \times\left|z^{\prime}\right|$
6. $\forall\left(z, z^{\prime}\right) \in \mathbb{C} \times \mathbb{C}^*$ : $\left|\dfrac{z}{z^{\prime}}\right|=\dfrac{|z|}{\left|z^{\prime}\right|}$
   1. $\forall\left(z, z^{\prime}\right) \in \mathbb{C}^2$, $\left|z+z^{\prime}\right| \leq|z|+\left|z^{\prime}\right|$
   2. Si $|z|=1$ alors $\bar{z}=\dfrac{1}{z}$
   3. Soit $\rm A$ un point donné du plan complexe d'affixe $z_{\mathrm A}$ et $\rm R$ un nombre réel positif. L'ensemble des points $\mathrm M$ du plan complexe d'affixe $z$ telle que : $\left|z-z_{\mathrm A}\right|=\mathrm R$ est le CERCLE de centre $\mathrm A$ et de rayon $\mathrm R$.
   4. Soit $\mathrm A$ et $\mathrm B$ deux points donnés du plan complexe d'affixes respectives $z_{\mathrm A}$ et $z_{\mathrm B}$. L'ensemble des points $\mathrm M$ du plan complexe d'affixe $z$ telle que : $\left|z-z_{\mathrm A}\right|=\left|z-z_{\mathrm B}\right|$ est la MEDIATRICE du segment $\rm [AB]$.
   5. Soit $\mathrm A$ un point donné du plan complexe d'affixe $z_{\mathrm A}$ et $\mathrm R$ un nombre réel positif. L'ensemble des points $\mathrm M$ du plan complexe d'affixe $z$ telle que : $\left|z-z_{\mathrm A}\right| \leq \mathrm R$ est le DISQUE de centre $\mathrm A$ et de rayon $\mathrm R$.

1. Racines carrées d'un nombre complexe non nul

Définition : Soit $a$ un nombre complexe non nul. On appelle racine carrée de $a$ tout nombre complexe $z$ tel que $z^2=a$.

Théorème : Tout nombre complexe non nul admet exactement deux racines carrées complexes opposées.

Recherche des racines carrées d'un nombre complexe par une méthode algébrique
Pour chercher les racines carrées d'un nombre $a$ complexe sous forme algébrique :

• On désigne par $z=x+i y$ une telle racine carrée. Alors $x$ et $y$ sont solutions du système suivant :
  $$\left\{\begin{array}{l} x^2-y^2=\operatorname{Re}(a) \\ 2 x y=\operatorname{Im}(a) \\ x^2+y^2=|z| \end{array}\right.$$
• On commence par résoudre le système formé par les deux équations (1) et (3) qui a a priori quatre couples $(x, y)$ solutions.
• Et compte tenu de l'équation (2), on ne retient que les deux couples $(x, y)$ tels que le signe de $x y$ soit celui de $\operatorname{Im}(a)$.

On se gardera d'appliquer cette méthode dans le cas où $a$ est un nombre réel. Les racines carrées de $a$ sont alors évidentes, égales à $\pm \sqrt{a}$ si $a$ est positif et à $\pm i \sqrt{|a|}$ si $a$ est négatif.

2. Équations du second degré dans $\mathbb{C}$

On appelle ainsi toute équation de la forme $a z^2+b z+c=0$, où $a$, $b$, $c$ sont trois nombres complexes donnés, avec $a \neq 0$.

Théorème : Soit $a$, $b$, $c$ des nombres complexes avec $a \neq 0$.

L'équation $a z^2+b z+c=0$ admet dans $\mathbb{C}$, deux solutions (éventuellement confondues), à savoir :

$z_1=\dfrac{-b+\delta}{2 a}$ et $z_2=\dfrac{-b-\delta}{2 a}$

où $\delta$ est une racine carrée de la quantité $\Delta=b^2-4 a c$ appelée discriminant.

3. Cas d'équations de degré supérieur ou égal à 3

Théorème : Soient $a_1$, $a_2$, $\ldots$, $a_{n}$ des nombres complexes avec $a_{n} \neq 0$ et $n \geq 2$.

Soit $\mathrm P(z)=a_n z^n+a_{n-1} z^{n-1}+\ldots+a_1 z+a_0$. Si $z_0$ est une racine de $\rm P$, alors $\mathrm P(z)=\left(z-z_0\right) \mathrm Q(z)$, où $\rm Q$ est un polynôme de degré $n-1$.

Conséquence : Dans la pratique, la résolution des équations de degré 3 ou 4 se ramène souvent à celles d'équations du premier et du second degré.

1. Argument d’un nombre complexe non nul

Le plan complexe est rapporté au repère orthonormé direct $(\mathrm O, \vec{u}, \vec{v})$.

Définition : Soit $z$ un nombre complexe non nul d'image $\mathrm M$ dans le plan complexe. Un argument $\theta$ de $z$ est une mesure en radians de l'angle $(\vec{u}, \overrightarrow{\rm O M})$.

Propriétés : Soit $z$ et $z^{\prime}$ des éléments de $\mathbb{C}^*=\mathbb{C} \backslash\{0\}$ et $n$ un relatif entier. Alors, on a :

1. $\arg \left(z z^{\prime}\right)=\arg (z)+\arg \left(z^{\prime}\right)[2 \pi]$
2. $\arg \left(\dfrac{1}{z}\right)=-\arg (z)[2 \pi]$
3. $\arg \left(\dfrac{z}{z^{\prime}}\right)=\arg (z)-\arg \left(z^{\prime}\right)[2 \pi]$
4. $\arg \left(z^n\right)=n \arg (z)[2 \pi]$
5. $\arg (-z)=\arg (z)+\pi[2 \pi]$
6. $\arg (\bar{z})=-\arg (z)[2 \pi]$

2. Forme trigonométrique d'un nombre complexe

Soit $z$ un nombre complexe non nul. Soit $\theta$ une mesure de l'angle $(\vec{u}$, $\overrightarrow{\rm O M})$. Alors, on a :

$z=|z|(\cos \theta+i \sin \theta)$

Cette écriture s'appelle forme trigonométrique du nombre complexe $z$.
On écrit aussi $z=[r, \theta]$.

Attention ! Le nombre complexe nul $z=0$ ne possède pas d'arguments car dans ce cas, l'angle $(\vec{u}, \overrightarrow{\rm O M})$ n'est pas défini puisqu'on ne définit que l'angle d'un couple de vecteurs non nul.

Théorème :

Deux nombres complexes sont égaux si et seulement s'ils ont le même module et le même ensemble d'arguments.

Conséquence :

Pour trouver une forme trigonométrique d'un nombre complexe non nul, il suffit de calculer son module et un de ses arguments.

Théorème :

$\boxed{z=r(\cos (\theta)+i \sin (\theta)) \text { avec } r>0 \Leftrightarrow r=|z| \text{ et }  \theta=\arg (z) ~(\bmod 2 \pi)}$

On pose par analogie des opérations sur l’argument avec la fonction exponentielle :

$\cos \theta+i \sin \theta=\mathrm e^{i \theta}$

Définition : (Forme exponentielle).

Un nombre complexe $z$ de module $r$ et d'argument $\theta$ s'écrit : $z=r \mathrm e^{i \theta}$. Cette écriture est appelée notation exponentielle de $z$.

Théorème :

Pour tous réels $\theta$ et $\theta^{\prime}$ de $\mathbb{R}$ et tout entier relatif $n$, on a :

1. $\mathrm e^{i \theta} \times \mathrm e^{i \theta^{\prime}}=\mathrm e^{i\left(\theta+\theta^{\prime}\right)}$
2. $\dfrac{\mathrm e^{i \theta}}{\mathrm e^{i \theta^{\prime}}}=\mathrm e^{i\left(\theta-\theta^{\prime}\right)}$
3. $\left(\mathrm e^{i \theta}\right)^n=\mathrm e^{i n \theta}$

La relation (3) est souvent appelée formule de Moivre.

Formules d'EULER

$\cos \theta=\dfrac{\mathrm e^{i \theta}+\mathrm e^{-i \theta}}{2}$ et $\sin \theta=\dfrac{\mathrm e^{i \theta}-\mathrm e^{-i \theta}}{2}$

• Pour exprimer $\cos n x$ et $\sin n x$ comme polynôme en $\cos x$ et $\sin x$, on écrit, d'après la formule de Moivre : $(\cos \theta+i \sin \theta)^n=\cos n \theta+i \sin n \theta$, puis on développe le premier membre par la formule du binôme. Ensuite, on identifie les parties réelles et imaginaires de chaque membre.
• Pour linéariser un polynôme trigonométrique, c'est-à-dire exprimer des expressions du type $f(x)= \cos ^p x \sin ^q x$ comme somme de termes de la forme $a_n \cos n x+b_n \sin n x$, on procédera comme suit :
  • Écrire $f(x)$ en fonction de $e^{i x}$ et $e^{-i x}$ en utilisant les formules d'Euler.
  • Développer les parenthèses aux puissances $p$ et $q$ en utilisant la formule du binôme. Dans le cas de petits exposants, on utilisera avec profit le triangle de Pascal.
  • Développer le produit des deux parenthèses.
  • Regrouper les exponentielles conjuguées et appliquer à nouveau (mais en sens inverse) les formules d'Euler.

Transformation de $\boldsymbol{a \cos x+b \sin x}$

Posons $z=a+i b$ que nous écrivons sous forme exponentielle :

$z=r \mathrm e^{i \theta}$ avec $r>0$ et  $\theta \in \mathbb{R}$

En remarquant que $a \cos x+b \sin x=\operatorname{Re}\left(\bar{z} \mathrm e^{i x}\right)=r \operatorname{Re}\left(\mathrm e^{-i \theta} \mathrm e^{i x}\right)=r \operatorname{Re}\left(\mathrm e^{i(x-\theta)}\right)$.

Alors $a \cos x+b \sin x=r \cos (x-\theta)=\sqrt{a^2+b^2} \cos (x-\theta)$ où $\theta$ est un argument de $z$.

Formules de factorisation

On a $\mathrm e^{i \alpha}+\mathrm e^{i \beta}=\mathrm e^{i \frac{\alpha+\beta}{2}}\left(\mathrm e^{i \frac{\alpha-\beta}{2}}+\mathrm e^{-i \frac{\alpha-\beta}{2}}\right)=2 \cos \left(\dfrac{\alpha-\beta}{2}\right) \mathrm e^{i \frac{\alpha+\beta}{2}}$

En séparant partie réelle et partie imaginaire de chaque membre et en les identifiant, on obtient les formules donnant $\cos \alpha+\cos \beta$ et $\sin \alpha+\sin \beta$.

De même, $\mathrm e^{i \alpha}-\mathrm e^{i \beta}=\mathrm e^{i \frac{\alpha+\beta}{2}}\left(\mathrm e^{i \frac{\alpha-\beta}{2}}-\mathrm e^{-i \frac{\alpha-\beta}{2}}\right)=2 i \sin \left(\dfrac{\alpha-\beta}{2}\right) \mathrm e^{i \frac{\alpha+\beta}{2}}$
Par identification des parties réelles et parties imaginaires de chaque membre, on obtient les formules donnant $\cos \alpha-\cos \beta$ et $\sin \alpha-\sin \beta$.

Théorème et définition : Étant donné le nombre complexe non nul $\rm W = r \exp(i\theta)$, il existe $n$ nombres distincts $\rm Z$ tels que $\mathrm Z^n=\mathrm W$. Ces nombres sont appelés les racines n-ièmes de $\mathrm W$. Ils sont donnés par :

$\mathrm Z_k=\left[\sqrt[n]{r} ~; \dfrac{\theta}{n}+\dfrac{2 k \pi}{n}\right]$ $=\sqrt[n]{r} \exp \left[i\left(\dfrac{\theta}{n}+\dfrac{2 k \pi}{n}\right)\right]$ 

avec $0 \leq k \leq n-1$

Dans le plan complexe muni du repère orthonormé $(\mathrm O, \vec{u}, \vec{v})$, les images des racines n-ièmes d'un nombre complexe non nul $\boldsymbol{a}$ forment un polygone régulier à $\boldsymbol{n}$ côtés inscrit dans un cercle de centre $\mathbf{O}$ et de rayon $\boldsymbol{\sqrt[n]{|a|}}$.

Cas particulier : Racines n-ièmes de l'unité

Théorème et définition : Pour tout entier naturel non nul $n$, l'équation $z^n=1$ admet $n$ racines distinctes définies par $\mathrm Z_k=\mathrm e^{i \frac{2 k\pi}{n}}$, l'entier $k$ appartenant à $\{0{,}1, \ldots, n-1\}$. Les solutions (ou racines) de l'équation $z^n=1$ sont appelées racines n-ièmes de l'unité.

La somme de toutes les racines de 1 est nulle.

Théorème : On obtient les $n$ racines n-ièmes d'un nombre complexe non nul en multipliant l'une quelconque d'entre elles par les $n$ racines n-ièmes de l'unité.

1. Angles orientés et nombres complexes

Théorème : Soient $\vec{u}$ et $\vec{u}^{\prime}$ deux vecteurs non nuls d'affixes respectives $z$ et $z^{\prime}$.

Alors :

1. $\left|\dfrac{z^{\prime}}{z}\right|=\dfrac{\left\|\vec{u}^{\prime}\right\|}{\|\vec{u}\|}$
2. $\arg \left(\dfrac{z^{\prime}}{z}\right)=\left(\vec{u}, \vec{u}^{\prime}\right)[2 \pi]$
3. $(\vec{u}$ et $\vec{u}^{\prime}$ sont colinéaires) $\Leftrightarrow\left(\vec{u}, \vec{u}^{\prime}\right)=0[\pi]$ $\Leftrightarrow \arg \left(\dfrac{z^{\prime}}{z}\right)=0[\pi]$ $\Leftrightarrow \dfrac{z^{\prime}}{z}$ est réel.
4. $(\vec{u}$ et $\vec{u}^{\prime}$ sont orthogonaux) $\Leftrightarrow\left(\vec{u}, \vec{u}^{\prime}\right)=\dfrac{\pi}{2}[\pi]$ $\Leftrightarrow \arg \left(\dfrac{z^{\prime}}{z}\right)=\dfrac{\pi}{2}[\pi]$ $\Leftrightarrow \dfrac{z^{\prime}}{z}$ est imaginaire pur.

Conséquences :

Soient $\rm A$, $\rm B$, $\rm C$, $\rm D$ des points distincts du plan complexe d'affixes respectives $z_{\mathrm A}$, $z_{\mathrm B}$, $z_{\mathrm C}$ et $z_{\mathrm D}$.

1. $(\overrightarrow{\rm A B}$, $\overrightarrow{\rm C D})=\arg \left(\dfrac{z_{\mathrm D}-z_{\mathrm C}}{z_{\mathrm B}-z_{\mathrm A}}\right)$
2. $\rm A$, $\rm B$, $\rm C$ sont alignés si et seulement si $\dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}} \in \mathbb{R} \Leftrightarrow \arg \left(\dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}}\right)=0[\pi]$
3. Le triangle $\rm A B C$ est rectangle en $\mathrm A$ si et seulement si $\rm (A B) \perp(A C)$ ce qui équivaut à :
   $\rm \overrightarrow{A B} \perp \overrightarrow{A C}$ $\Leftrightarrow \dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}} \in i \mathbb{R}$ $\Leftrightarrow \arg \left(\dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}}\right)=\dfrac{\pi}{2}[\pi]$
4. Le triangle $\rm ABC$ est rectangle et isocèle en $\mathrm A$ si et seulement si $\dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}}=\mathrm e^{ \pm i \dfrac{\pi}{2}}= \pm i$.
5. Le triangle $\rm ABC$ est équilatéral si et seulement si $\dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}}=\mathrm e^{ \pm i \frac{\pi}{3}}$ ou encore à :
   $\dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}}=j^2$ ou $\dfrac{z_{\mathrm C}-z_{\mathrm A}}{z_{\mathrm B}-z_{\mathrm A}}=-j$ où $j$ est le nombre complexe $-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i$.
6. $\arg \left(z-z_{\mathrm A}\right)=\theta[2 \pi]$ si et seulement si le point $\mathrm M$ d'affixe $z$ appartient à la demi-droite d'origine $\mathbf A$ et faisant un angle de $\boldsymbol{\theta}$ modulo $\boldsymbol{2 \pi}$ avec $\boldsymbol{\left(\mathrm O, \overrightarrow{\mathrm e_1}\right)}$ dans un repère orthogonal $\rm (O~;\vec {e_1}~;\vec {e_2})$
7. $\arg \left(z-z_{\mathrm A}\right)=\theta[\pi]$ si et seulement si le point $\mathrm{M}$ d'affixe $z$ appartient à la droite contenant $\rm A$ faisant un angle de $\boldsymbol{\theta}$ modulo $\boldsymbol{\pi}$ avec $\boldsymbol{\left(\mathbf{O}, \overrightarrow{\mathrm e_1}\right)}$ dans un repère orthogonal $\rm (O~;\vec {e_1}~;\vec {e_2})$.
8. $\rm ABCD$ est un rectangle si et seulement si $\rm ABCD$ est un parallélogramme et $\rm AC=BD$.
9. $\rm ABCD$ est un carré si et seulement si $\rm ABCD$ est un parallélogramme et $\rm (AC) \perp(BD)$ et $\mathrm{AC}=\mathrm{BD}$.
10. L'ensemble des points $\rm M$ tels que $(\overrightarrow{\mathrm {M A}}$, $\overrightarrow{\mathrm{M B})}= 0[2 \pi]$ est la droite $\rm (AB)$ privée du segment $\rm [A B]$.
11. L'ensemble des points $\rm M$ tels que $(\overrightarrow{\rm M A}$, $\overrightarrow{\rm M B}) = 0 [\pi]$ est la droite $(\mathrm{AB})$ privée des points $\rm A$ et $\rm B$.
12. L'ensemble des points $\rm M$ tels que $(\overrightarrow{\rm MA}$, $\overrightarrow{\rm M B})=\pi[2 \pi]$ est le segment $\rm [AB]$ privé des points $\rm A$ et $\rm B$.
13. L'ensemble des points $\rm M$ tels que $(\overrightarrow{\rm M A}$, $\overrightarrow{\rm M B})=\dfrac{\pi}{2}[2 \pi]$ est le cercle de diamètre $\rm [A B]$ privé des points $\rm A$ et $\rm B$.

2. Complexes et transformation du plan

a) Fonction dans $\boldsymbol{\mathbb{C}}$ associée à une transformation du plan

Une transformation du plan complexe $\mathscr{P}$ est une application $\begin{aligned}f: \mathscr{P} & \rightarrow \mathscr{P} \\
\rm M & \mapsto \rm M^{\prime}\end{aligned}$ qui est bijective.

À toute transformation $f$ du plan complexe, on peut associer une unique application $\begin{aligned} \varphi: \mathbb{C} & \rightarrow \mathbb{C} \\ z & \mapsto z^{\prime} \end{aligned}$ telle que si $\mathrm M^{\prime}\left(z^{\prime}\right)=f(\mathrm M(z))$, alors $\varphi(z)=z^{\prime}$.

$\varphi$, qui est également bijective, est appelée transformation complexe associée à $f$. La formule $z^{\prime}=\varphi(z)$ est appelée écriture complexe de la transformation $f$.

b) Transformations élémentaires du plan

• La symétrie d'axe $\rm (OI)$ a pour écriture complexe $z^{\prime}=\bar{\rm z}$.
• La symétrie d'axe $\rm (OJ)$ a pour écriture complexe $z^{\prime}=-\bar{\rm z}$.
• La symétrie de centre $\rm O$ a pour écriture complexe $z^{\prime}=-\rm z$.

c) Translation

La translation du vecteur $\vec{u}$, d'affixe $a$, transforme un point $\rm M(z)$ en un point $\mathrm M'\left(z^{\prime}\right)$ tel que :

$z^{\prime}=z+a$

d) Homothétie

L'homothétie de centre $\Omega(\omega)$ et de rapport $k \in \mathbb{R}^*$ transforme un point $\mathrm M(z)$ en un point $\mathrm M^{\prime}\left(z^{\prime}\right)$ tel que : $z^{\prime}-\omega=k(z-\omega)$.

e) Rotation

La rotation de centre $\Omega(\omega)$ et d'angle $\theta$ transforme un point $\mathrm M(z)$ en un point $\mathrm M^{\prime}\left(z^{\prime}\right)$ tel que : $z^{\prime}-\omega= \mathrm e^{i \theta}(z-\omega)$.

f) Propriétés

Toute transformation du plan d'écriture complexe $z^{\prime}=a z+b$, avec $a \in \mathbb{C}^*$ et $b \in \mathbb{C}$ est :

• une translation de vecteur $\vec{u}$ d'affixe $b$ si $a=1$.
• une homothétie de centre le point $\Omega$ tel que $z_{\Omega}=\dfrac{b}{1-a}$ et de rapport $k=a$ si $a \in \mathbb{R}^* \backslash\{1\}$.
• une rotation de centre le point $\Omega$ tel que $z_{\Omega}=\frac{b}{1-a}$ et d'angle $\theta=\arg (a)[2 \pi]$ si $a \in \mathbb{C} \backslash$ $\mathbb{R}$ et $|a|=1$.

g) Similitude directe

On appelle similitude directe toute transformation du plan d'écriture complexe $z^{\prime}=a z+b$, avec $a$ $\in \mathbb{C}^*$ et $b \in \mathbb{C}$.

Les éléments caractéristiques de la similitude directe sont :

• son rapport $\lambda=|a|$.
• son angle $\theta=\arg (a)[2 \pi]$
• son centre le point $\Omega$ tel que $z_{\Omega}=\dfrac{b}{1-a}$ si $a \neq 1$.

Propriétés

• Une similitude directe est soit une translation, soit une homothétie, soit une rotation, soit la composée d'une rotation et d'une homothétie de même centre.
• L'homothétie, la rotation et la composition d'une rotation et d'une homothétie de même centre sont des similitudes directes qui ont pour point invariant leur centre.
• Soit $\rm S$ une similitude directe de rapport $k$.
  
  • $\rm S$ conserve : I'alignement, le parallélisme, l'orthogonalité, les angles orientés, les barycentres et le contact.
  • $\rm S$ multiplie : les longueurs par $k$ et les aires par $k^2$.
  • $\rm S$ transforme : les droites en droites, les demi-droites en demi-droites, les segments en segments et les cercles en cercles.