Fonction logarithme népérien

Définition et notations

La fonction logarithme népérien, notée $\ln$ est l'unique primitive sur $]0~; +\infty[$ de la fonction $x \mapsto \dfrac{1}{x}$ qui s'annule en $1$.

Pour tout $x$ de $]0~ ;+\infty[$, son image $\ln (x)$ se note $\ln x$.

Conséquences immédiates :

1. L'ensemble de définition de la fonction logarithme népérien est $]0~ ; +\infty[$.
2. $\ln 1=0$
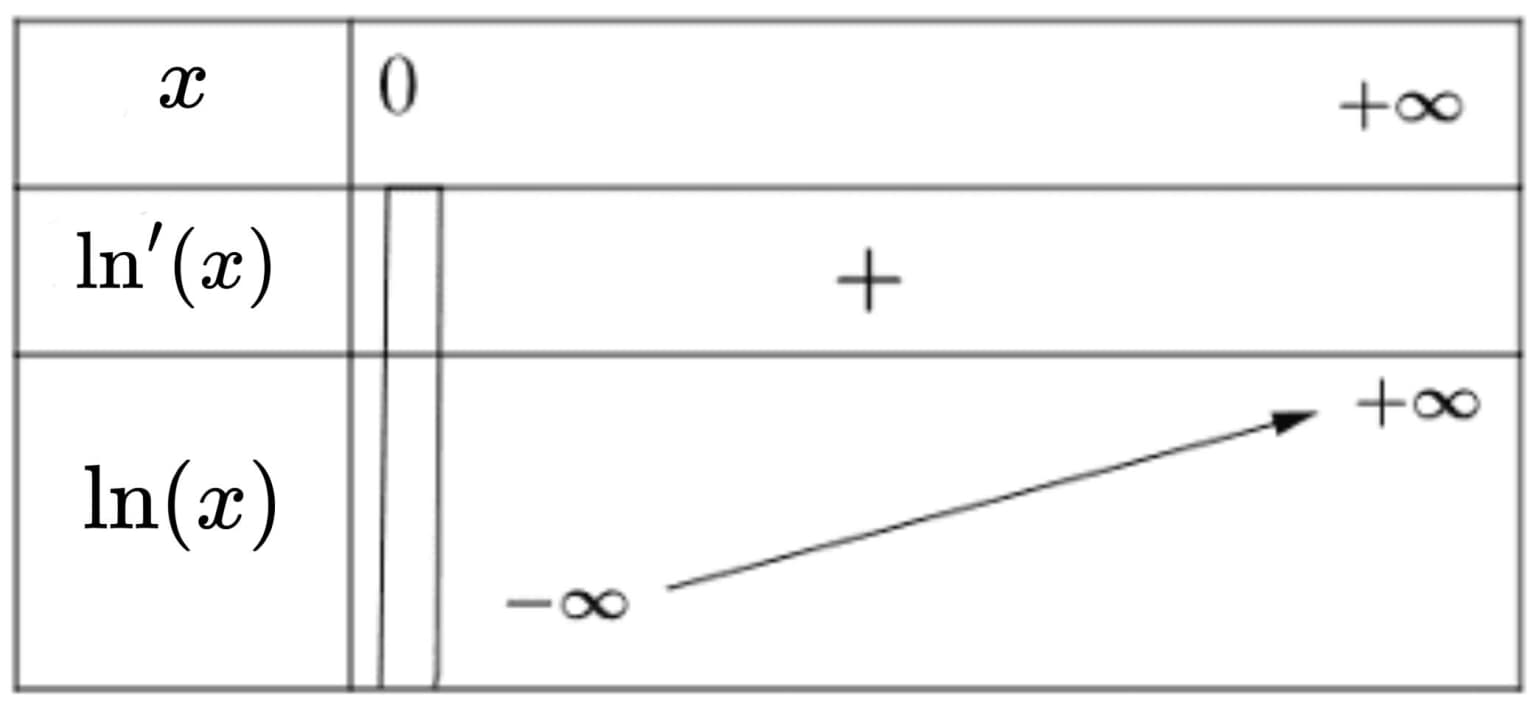
3. La fonction $\ln$ est dérivable sur $]0~ ;+\infty[$ et sur cet intervalle, sa dérivée est $x \mapsto \dfrac{1}{x}$. Ainsi : pour tout réel $x$ appartenant à $]0~ ;+\infty[$ : $\ln^{\prime}(x)=\dfrac{1}{x}$

Propriétés

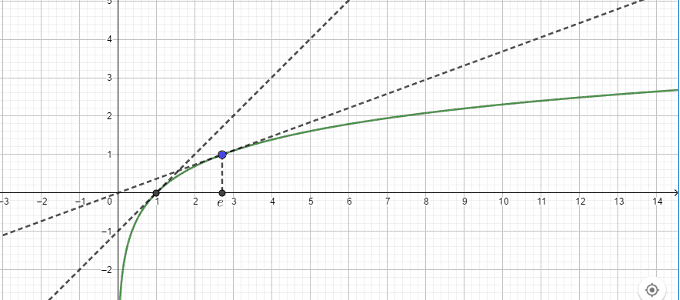
• La fonction $\ln$ est continue et strictement croissante sur $\bf{]0~; +\infty[}$.
• Pour tous réels $a$ et $b$ strictement positifs : $\ln a < \ln b \Leftrightarrow a < b$ et $\ln a = \ln b \Leftrightarrow a=b$

Théorème

Soit $u$ une fonction définie, dérivable et strictement positive sur un intervalle $I$.
Alors la fonction $\ln \circ u$ est définie et dérivable sur $\rm I$, et sa fonction dérivée est :

$(\ln \circ u)^{\prime}=\dfrac{u^{\prime}}{u}$

Corollaire

Si une fonction $u$ est dérivable et strictement positive sur un intervalle $\rm I$, alors les primitives de la fonction $\dfrac{u^{\prime}}{u}$ sont les fonctions $\mathrm F_k$ définies sur $\rm I$ par : $\mathrm F_k=(\ln \circ u)+k$, $k$ étant un réel arbitraire.

Théorème

Soit $u$ une fonction définie, dérivable et ne s'annulant pas sur un intervalle $\rm I$.
Alors la fonction $\ln \circ|u|$ est définie et dérivable sur $\rm I$, et sa fonction dérivée est :

$(\ln \circ|u|)^{\prime}=\dfrac{u^{\prime}}{u}$

Corollaire

Si une fonction $u$ est dérivable et ne s'annulant pas sur un intervalle $\rm I$, alors les primitives de la fonction $\dfrac{u^{\prime}}{u}$ sont les fonctions $\mathrm F_k$ définies sur $\rm I$ par : $\mathrm F_k=(\ln \circ|u|)+k$, $k$ étant un réel arbitraire.

1. Pour tous réels $a$ et $b$ strictement positifs, $\ln (a \times b)=\ln a+\ln b$
2. Pour tout réel $a$ strictement positif et pout tout entier relatif $n: \ln a^n=n \times \ln a$.

Corollaires

Pour tous réels $a$ et $b$ strictement positifs et pout tous $n$ et $p$ entiers relatifs :

1. $\ln \left(\dfrac{1}{a}\right)=-\ln a$
2. $\ln \left(\dfrac{a}{b}\right)=\ln a-\ln b$
3. $\ln \sqrt{a}=\dfrac{1}{2} \ln a$
4. $\ln \left(a^n \times b^p\right)=n \ln a+p \ln b$
5. $\ln \left(\dfrac{a^n}{b^p}\right)=n \ln a-p \ln b$

Rappelons que la fonction $\ln$ est, par définition, définie, continue et strictement croissante sur $] 0 ~;+\infty\left[=\mathbb{R}_{+}^*\right.$ et s'annule en $1$.

Sa fonction dérivée est la fonction $x \mapsto \dfrac{1}{x}$.

• Limites remarquables :
  • $\displaystyle \lim _{x \rightarrow+\infty} \ln x=+\infty$ et $\displaystyle \lim _{x \rightarrow 0^{+}} \ln x=-\infty$.
  • $\displaystyle \lim _{x \rightarrow+\infty}\left(\dfrac{\ln x}{x}\right)=0$, $\quad \displaystyle \lim _{x \rightarrow 0^{+}}(x \ln x)=0$
    et plus généralement, pour tout rationnel positif $a, \displaystyle \lim _{x \rightarrow+\infty}\left(\dfrac{\ln x}{x^a}\right)=0$ et $\displaystyle \lim _{x \rightarrow 0^{+}}\left(x^a \ln x\right)=0$.
  • $\displaystyle \lim _{x \rightarrow 0}\left(\dfrac{\ln (1+x)}{x}\right)=1$, ou de manière équivalente : $\displaystyle \lim _{u \rightarrow 1}\left(\dfrac{\ln u}{u-1}\right)=1$.
• Tableau de variation
  
• Bijection : La fonction $\ln$ est une bijection strictement croissante de $] 0 ~;+\infty[$ vers $\mathbb{R}$.
• Le nombre $\rm e$ : Le réel 1 admet un unique antécédent par la fonction $\ln$ ; ce nombre est noté $\rm e$.
  Le nombre $\rm e$ est donc l'unique réel tel que $\ln \mathrm{e}=1$.
  Une valeur approchée de $\rm e$ est $\mathrm{e} \approx 2,718$.
• Valeurs entières de la fonction $\ln$
  $\ln \mathrm{e}=1$, donc pour tout entier relatif $n$ et tout réel strictement positif $x$ :
  $\left\{\begin{array}{l}
  \ln \mathrm{e}^n=n \ln \mathrm{e}=n \\
  \ln x=n \Leftrightarrow x=\mathrm{e}^n
  \end{array}\right.$
• Tangentes particulières
  La courbe de la fonction In admet :
  
  • Au point de coordonnées $(1,0)$ une tangente d'équation $y=x-1$.
  • Au point $\mathrm{E}(\mathrm{e}, 1)$, une tangente d'équation $y=\dfrac{1}{\mathrm{e}} x$.
• Représentation graphique