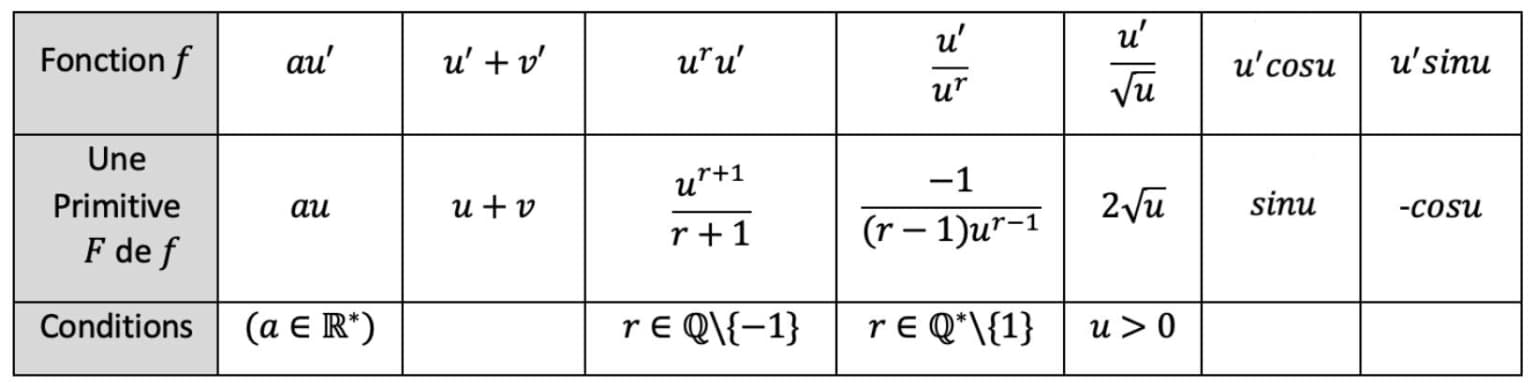Dérivées et primitives

Propriété :

Soit $u$ une fonction dérivable sur un intervalle $\rm I$ et $\rm v$ une fonction dérivable en $\rm J$ tel que :
pour tout $x \in \rm I$, $u(x) \in \mathrm{J}$.
La fonction composée $v \circ u$ est dérivable sur $\rm I$ et pour tout $x \in \rm I$,

$(v \circ u)^{\prime}(x)=v'(u(x))\times u'(x)$

Conséquences :

1. Si $u$ est une fonction dérivable sur l'intervalle $\rm I$, alors la fonction $u^n\left(n \in \mathbb{N}^*\right)$ est dérivable sur $\rm I$ et on a : $\left[u^n\right]^{\prime}=n u^{\prime} u^{n-1}$
2. Si $u$ est une fonction dérivable sur l'intervalle $\rm I$, alors les fonctions :
   $$x \mapsto \cos (u(x)), x \mapsto \sin (u(x))$$
   sont dérivables sur $\rm I$ et on a :
   $\begin{array}{ll}
   \forall x\in I = & {[\cos (u(x))]^{\prime}=-u^{\prime}(x) \sin (u(x))} \\ & (\cos u)^{\prime}=-u^{\prime} \sin u \\
   & {[\sin (u(x))]^{\prime}=u^{\prime}(x) \cos (u(x))} \\ & (\sin u)^{\prime}=u^{\prime} \cos u
   \end{array}$
3. Si $u$ est une fonction dérivable sur l'intervalle $\rm I$ et si pour tout $x \in\rm I$, $u(x) \neq \dfrac{\pi}{2}+k \pi$, $k \in \mathbb{Z}$, alors la fonction $x \mapsto \tan (u(x))$ est dérivable sur $\rm I$ et on a :
   $$[\tan (u(x))]^{\prime}=\dfrac{u^{\prime}(x)}{\cos ^2[u(x)]}=u^{\prime}(x)\left[1+\tan ^2 u(x)\right] \\ [\tan u]^{\prime}=\dfrac{u^{\prime}}{\cos ^2 u}=u^{\prime}\left[1+\tan ^2 u\right]$$
4. Si $u$ est une fonction dérivable et strictement positive sur l'intervalle $\rm I$, alors la fonction $\sqrt{u}$ : $x \mapsto \sqrt{u(x)}$ est dérivable sur $\rm I$ et on a :
   $$[\sqrt{u(x)}]^{\prime}=\dfrac{u^{\prime}(x)}{2 \sqrt{u(x)}} \\ (\sqrt{u})^{\prime}=\dfrac{u^{\prime}}{2 \sqrt{u}}$$

Théorème :

Soit $f$ une bijection d'un intervalle $\rm I$ sur un intervalle $\mathrm K=f(I)$ et $f^{-1}$ sa bijection réciproque.

Soit $y$ un nombre réel contenu dans $\rm K$ et $x$ le nombre réel de $\rm I$ tel que $f(x)=y$ (l'antécédent de $y$ par $f$).

On suppose que $f$ est dérivable au point $x$.

• Si $f^{\prime}(x)=0$ alors $f^{-1}$ n'est pas dérivable en $y$.
• Si $f^{\prime}(x) \neq 0$ alors $f^{-1}$ est dérivable en $y$ et on a : $\left(f^{-1}\right)^{\prime}(y)=\dfrac{1}{f^{\prime}(x)}$

La formule $\left(x^n\right)^{\prime}=n x^{n-1}$ reste valable pour tout $\mathrm{n} \in \mathbb{Q}$.

Avec la propriété précédente, cela donne : $\left(f^a\right)^{\prime}=a f^{a-1} f^{\prime}$ pour tout $a \in \mathbb{Q}$

1°) Soit $f$ une fonction dérivable sur un intervalle $\rm I$ et $f^{\prime}$ sa fonction dérivée sur $\rm I$.

Si $f^{\prime}$ est elle-même dérivable sur l'intervalle $\rm I$, la fonction dérivée de $f^{\prime}$ est appelée fonction dérivée seconde de la fonction $f$ et notée $f^{\prime \prime}$.

2°) Si $f^{\prime \prime}$ est à son tour dérivable, sa fonction dérivée est notée $f^{\prime \prime \prime}$, etc.

On obtient ainsi la notion de fonction dérivée $n$–ième, notée $f^{(n)}$ ou $\dfrac{d^n f}{d x^n}$.

Soit $f$ une fonction dérivable en un point $x_0$ de son domaine de définition, $(\mathrm{T})$ la tangente à $\mathrm{C}_{f}$ en $\mathrm{M}_0(x_0~ ; f(x_0))$. On dit que $\rm M$ est un point d'inflexion si $\mathrm{C}_{f}$ change de position par rapport à $\bf (T)$ en $\rm M$ (on dit aussi qu'elle traverse sa tangente en $\rm M)$. Il y a deux critères pour reconnaître un point d'inflexion :

Critère 1 : Si $f'$ s'annule sans changer de signe en $x_0$, alors $\mathrm{M}_0$ est un point d'inflexion.

Exemple : $f(x)=x^3$ en $0$.

Critère 2 : Si $f$ est deux fois dérivable en $x_{0}$ et si $f^{\prime \prime}$ s'annule en changeant de signe en $x_0$, alors $\mathrm{M}_0$ est un point d'inflexion.

Exemple : $f(x)=\dfrac{x^3}{x+1}$ en $0$.

Soit $f$ une fonction continue sur l'intervalle $[a, b]$ et dérivable sur l'intervalle $]a, b[$. Si la fonction dérivée $f^{\prime}$ admet au point $a$ une limite $l$, finie ou non, alors on a également :

$\displaystyle \lim _{x \rightarrow a}\left[\dfrac{f(x)-f(a)}{x-a}\right]=l$

1°) Définition

Soit $f$ et $\rm F$ deux fonctions définies sur un intervalle $\rm I$. On dit que $\rm F$ est une primitive de $f$ sur $\rm I$ lorsque $\rm F$ est dérivable sur $\rm I$ et, pour tout $x$ de $\rm I$, $\mathrm F^{\prime}(x)=f(x)$.

2°) Théorème

Toute fonction continue sur un intervalle $\rm I$ admet au moins une primitive sur $\rm I$.

3°) Théorème

Soit $f$ une fonction continue sur un intervalle $\rm I$. Si $\rm F$ et $\rm G$ sont deux primitives de $f$ sur $\rm I$, alors la fonction $\rm (F-G)$ est une constante sur $\rm I$.

Si donc l'on connait une primitive donnée $\rm F$ de $f$, alors l'ensemble des primitives de f sur I est l'ensemble des fonctions de la forme $\mathrm F+k$, où $k$ est une constante réelle arbitraire.

Corollaire :

Soit $f$ une fonction continue sur un intervalle $\rm I$. Soit $x_0$ un réel de $\rm I$ et un réel $y_0$. Alors il existe une unique primitive $\rm F$ de $f$ sur $\rm I$ telle que : $\mathrm F\left(x_0\right)=y_0$.

4°) Primitives des fonctions usuelles

5°) Opérations sur les primitives

6°) Primitives des fonctions du type $(g’\circ f).f’$

Soient $f$ et $g$ deux fonctions telles que $f$ soit dérivable sur l'intervalle $\rm I$ et $g$ dérivable sur $f(I)$ (ou sur un intervalle contenant $f(\rm I)$).

Alors la fonction $\left(g^{\prime} \circ f\right) \times f^{\prime}$ a pour primitives sur $\rm I$ les fonctions de la forme :

$g \circ f+\rm C, \quad C \in \mathbb{R}$

Théorème :

Soit $f$ une fonction continue sur un intervalle $[a~;b]$ et dérivable sur $]a~;b[$. On suppose que $a < b$ et qu'il existe deux constantes $m$ et $\rm M$ telles que, pour tout $x$ de $[a~; b]$, on ait : $\color{orangered}{m \leq f^{\prime}(x) \leq \mathrm M}$. Alors, on a la double inégalité suivante :

$m(b-a) \leq f(b)-f(a) \leq M(b-a)$.

Corollaire : Soit $f$ une fonction continue sur un intervalle $[a~;b]$ et dérivable sur $]a~;b[$. On suppose qu'il existe une constante $k$ telle que pour tout $x$ de $[a~ ; b]$, on $a :\left|f^{\prime}(x) \right | \leq k$.

Alors, on a : $|f(b)-f(a)| \leq k|b-a|$.