Calcul intégral

1. Définition et notations

Définition

Soit $f$ une fonction continue sur un intervalle fermé borné $\mathrm{I}=[a, b]$, F une primitive quelconque de $f$ sur $\rm I$.

On appelle « intégrale de $a$ à $b$ de $f$ » le réel $\mathrm{F}(b)-\mathrm{F}(a)$ (on montre qu'il est indépendant du choix de $\mathrm F$ et qu'il ne dépend que de la fonction $f$ et des nombres $a$ et $b)$.

Notations et remarques :

• Les réels $a$ et $b$ sont appelés les « bornes » de l'intégrale.
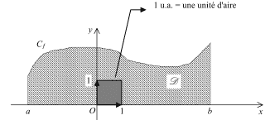
• On note l'intégrale $\displaystyle \int_a^b f(x) d x$.
• Pour écrire l'intégrale, on utilise aussi la notation $\big [\mathrm F(x)\big]_a^b$.
  D'où $\displaystyle\int_a^b f(x) d x=\big[\mathrm F(x)\big]_a^b$ $=\mathrm F(b)-\mathrm F(a)$.
• Dans la notation $\displaystyle \int_a^b f(x) dx$, on peut remplacer la lettre $x$ par n'importe quelle autre lettre.
  Ainsi : $\displaystyle \int_a^b f(x) d x=\displaystyle \int_a^b f(t) dt$.
• Si $f$ est une fonction continue sur un intervalle $\rm I$ contenant les réels $a$ et $b$ (avec $b < a$), on pose par convention $\displaystyle \int_a^b f(x) d x=-\int_b^a f(x) d x$

2. Propriétés de l'intégrale

Propriété 1 : Linéarité

Soient $f$ et $g$ deux fonctions numériques définies et continues sur un intervalle $\rm I$ et soient $a$ et $b$ des éléments de $\rm I$.

1. Soit $\lambda \in \mathbb{R}$ : $\displaystyle \int_a^b(\lambda f(x)) d x=\lambda \int_a^b f(x) d x$ (1^re formule de linéarité).
   2. $\displaystyle\int_a^b(f+g)(x) d x=\int_a^b f(x) d x+\int_a^b g(x) d x$ (2^nde formule de linéarité).

Il en résulte que $\displaystyle \int_a^b(\lambda f+\mu g)(x) d x=\lambda \int_a^b f(x) d x+\mu \int_a^b g(x) d x$ pour tous réels $\lambda$ et $\mu$.

Propriété 2 : Relation de CHASLES

Soit $f$ une fonction continue sur un intervalle $\rm I$ contenant les réels $a$, $b$ et $c$.

On a alors $\displaystyle \int_a^b f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$.

Propriété 3 : Intégrale et inégalités

Soit $f$ et $g$ deux fonctions continues sur $[a, b]$.

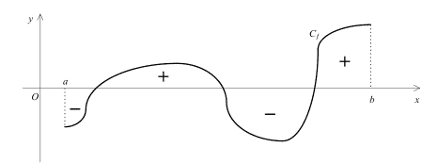
• Positivité : Si, pour tout réel $x$ de $[a, b]$, on a $f(x) \geq 0$, alors $\int_a^b f(x) d x \geq 0$.
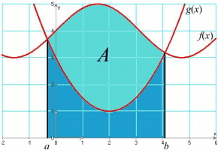
  Autrement dit, si $f$ est positive sur $[a, b]$, alors $\displaystyle\int_a^b f(x) d x$ est un réel positif.
• Intégration d'une inégalité : Si pour tout réel $x$ appartenent à $[a, b]$, on a $f(x) \leq g(x)$, alors on a : $\displaystyle \int_a^b f(x) d x \leq \int_a^b g(x) d x$
• Inégalités de la moyenne : Si $m$ et $\rm M$ sont deux réels tels que, pour tout réel $x$ appartenant à $[a, b]$, $m \leq f(x) \leq \rm M$, alors on a : $\displaystyle m(b-a) \leq \int_a^b f(x) d x \leq \mathrm M(b-a)$.

Attention : Les résultats de ce théorème ne sont valables qu'avec la condition $\color{orange}{\boldsymbol{a \leq b}}$.

Corollaire 1 (Majoration) : Si $\rm M$ est un réel strictement positif tel que : pour tout réel $x$ appartenant à $[a, b]$, on a : $|f(x)| \leq \rm M$, alors : $\displaystyle \left|\int_a^b f(x) d x\right| \leq \mathrm M|b-a|$.

Corollaire 2 (Comparaison) : Soit $f$, $g$ et $h$ trois fonctions continues sur un intervalle $[a, b]$ et telles que, pour tout $x \in [a, b]$, on ait : $h(x) \leq f(x) \leq g(x)$.
Alors, on a : $\displaystyle \int_a^b h(x) d x \leq \int_a^b f(x) d x \leq \int_a^b g(x) d x$.

Corollaire 3 (Valeur absolue) : Soit $f$ une fonction continue sur $[a, b]$, alors $\displaystyle \left|\int_a^b f(x) d x\right| \leq \int_a^b|f(x)| d x$.

Propriété 4 : Valeur moyenne
Soit $f$ une fonction continue sur $[a,b]$.
La valeur moyenne de $f$ est :
$\displaystyle\frac{1}{b-a}\int_a^b f(x)dx$

Théorème : Intégration par parties

Si $u$ et $v$ sont deux fonctions dérivables sur un intervalle $\rm I$ et telles que les fonctions dérivées $u^{\prime}$ et $v^{\prime}$ soient continues sur $\rm I$.

Alors, pour tout couple $(a, b)$ d'éléments de $\rm I$, on a :

$\displaystyle \int_a^b u(x) v^{\prime}(x) d x$ $\displaystyle =\big[u(x) v(x)\big]_a^b-\int_a^b v(x) u^{\prime}(x) d x$

1. Unité d'aire

Soit $(\mathrm O, \vec{\imath}, \vec{\jmath})$ un repère orthogonal. On considère les points : $\rm A(1~ ; 0)$, $\rm B(0 ~; 1)$ et $\rm C(1 ; 1)$.

On convient de prendre pour unité d'aire l'aire du rectangle $\rm OACB$.

L'unité d'aire, souvent notée $\rm u . a$ est : $\mathrm{1 u. a.} = \|\vec{\imath}\| \times\|\vec{\jmath}\|$.

2. Cas d'une fonction positive

Théorème (admis)

Soit $f$ une fonction continue et positive sur un intervalle $[a, b]$, c'est-à-dire telle que pour tout réel $x$ appartenant à $[a, b]$, $f(x) \geq 0$.

L'aire $\mathscr{A}$, exprimée en unités d'aire, de l'ensemble $\mathscr{D}$ de tous les points dont les coordonnées $(x, y)$ vérifient $a \leq x \leq b$, et $0 \leq y \leq f(x)$ est $\displaystyle\mathscr{A}=\int_a^b f(x) d x$.

3. Cas d'une fonction négative

Théorème (admis)

Soit $f$ une fonction continue et négative sur un intervalle $[a, b]$, c'est-à-dire telle que pour tout réel $x$ appartenant à $[a, b]$, $f(x) \leq 0$.

L'aire $\mathscr{A}$, exprimée en unités d'aire, de l'ensemble $\mathscr D$ de tous les points dont les coordonnées $(x, y)$ vérifient $a \leq x \leq b$, et $f(x) \leq y \leq 0$ est $\displaystyle\mathscr{A}=\int_a^b(-f(x)) d x$.

4. Cas d'une fonction de signe quelconque

Soit $f$ une fonction continue sur l'intervalle $[a, b]$. $\displaystyle \int_a^b f(x) d x$ se calcule en comptant positivement l'aire des domaines où $f$ est positive et négativement l'aire des domaines où $f$ est négative.

5. Aire d'une surface délimitée par deux courbes

Théorème (admis)

Soit $f$ et $g$ deux fonctions continues sur un intervalle $[a, b]$, et telles que pour tout réel $x$ appartenant à $[a, b]$, $f(x) \leq g(x)$.

L'aire $\mathscr{A}$, exprimée en unités d'aire, de l'ensemble $\mathscr D$ de tous les points dont les coordonnées $(x, y)$ vérifient $a \leq x \leq b$, et $f(x) \leq y \leq g(x)$ est $\displaystyle \mathscr{A}=\int_a^b(g(x)-f(x)) d x$.

6. Calculs de volumes

L'espace étant muni d'un repère orthogonal $(\mathrm O, \vec{\imath}, \vec{\jmath}, \vec{k})$, on considère un solide délimité par des plans parallèles d'équations $z=a$ et $z=b$. Si la fonction $\rm S$ qui, à toute cote $z$ associe l'aire de la section contenue dans le plan perpendiculaire à l'axe $(\mathrm O, \vec{k})$ est continue sur $[a~ ; b]$, alors le volume $\mathscr{V}$ du solide est donné par la formule :

$\displaystyle \mathscr{V}=\int_a^b \mathrm S(z) d z \text { u.v. }$

(L'unité de volume u.v. est le volume du parallélépipède unité.)

Cas particulier : Volume d'un solide de révolution

L'espace est muni d'un repère orthogonal $(\mathrm O, \vec{\imath}, \vec{\jmath}, \vec{k})$.

On considère dans le plan $(\mathrm O, \vec{\imath}, \vec{\jmath})$ un arc $\rm A B$ d'une courbe d'équation $y=f(x)$ et dont les extrémités $\rm A$ et $\rm B$ ont pour coordonnées dans ce plan $\mathrm{A}(a, f(a))$ et $\mathrm{B}(b, f(b))$ (où $f$ est une fonction continue et positive sur $[a~; b]$ ).

La rotation de l'arc $\rm A B$ autour de l'axe $(\mathrm O, \vec{\imath})$ engendre une surface appelée surface de révolution $(\rm S)$ (voir figure ci-dessous).

La partie de l'espace limitée par la surface $\rm (S)$ et les plans d'équations $x=a$ et $x=b$ est appelée solide de révolution de surface $\rm (S)$.

Le volume $\mathscr V$ de ce solide de révolution est $\displaystyle\mathscr{V}=\pi \int_a^b f^2(x) d x$.