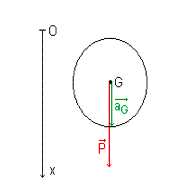
Un solide est dit en chute libre s’il est soumis uniquement à son poids (le fait qu’il n’existe pas de force de frottement impose que cette condition ne peut être réalisée que dans le vide).
- Equation différentielle du mouvement
Système étudié : le solide
Référentiel utilisé : le repère galiléen
Bilan des forces extérieures : $\vec P$ poids du solide
On appliquant la deuxième loi de Newton :
$\sum \overrightarrow{ F}_{ext} = m \overrightarrow{a}$
$\quad \Longrightarrow \overrightarrow{ P} = m \overrightarrow{ a_g}$
$\quad \Longrightarrow m \vec g = m \vec a_g$
$\quad \Longrightarrow \vec g = \vec a_g$
- Résolution de l’équation différentielle
Conditions initiales : supposons que la position initiale (à l’instant $𝑡 = 0$) du solide soit $x_0$ et sa vitesse initiale soit : $v_{x0}$
Expression de la vitesse
$\dfrac{dv_x}{dt} = g \Rightarrow v_x = gt + k$
À $t = 0,\: v_x = v_{x0} \Rightarrow v_{x0} = g \times 0 + k \Rightarrow v_{x0} = k$
D’où :
$v_x = gt + v_{x0}$
Remarque : si la vitesse initiale est nulle $(v_{x_0} = 0)$, alors l’expression de la vitesse devient $v_x = gt$.
Expression de position
$v_x = \dfrac{dOM}{dt} \Rightarrow \dfrac{dOM}{dt} = gt + v_{x0}$
$\Rightarrow x = x = \dfrac{1}{2} g t^2 + v_{x0} t + k$
$\quad$ À $t = 0, \:x = x_0 \Rightarrow x_0 = \dfrac{1}{2} g 0^2 + v_{x0} 0 + k$
D’où $x_0 = k$
D’où :
$x = \dfrac{1}{2} gt^2 + v_{x0} t + x_0$