Définition et notations
La fonction logarithme népérien, notée $\ln$ est l'unique primitive sur $]0~; +\infty[$ de la fonction $x \mapsto \dfrac{1}{x}$ qui s'annule en $1$.
Pour tout $x$ de $]0~ ;+\infty[$, son image $\ln (x)$ se note $\ln x$.
Conséquences immédiates :
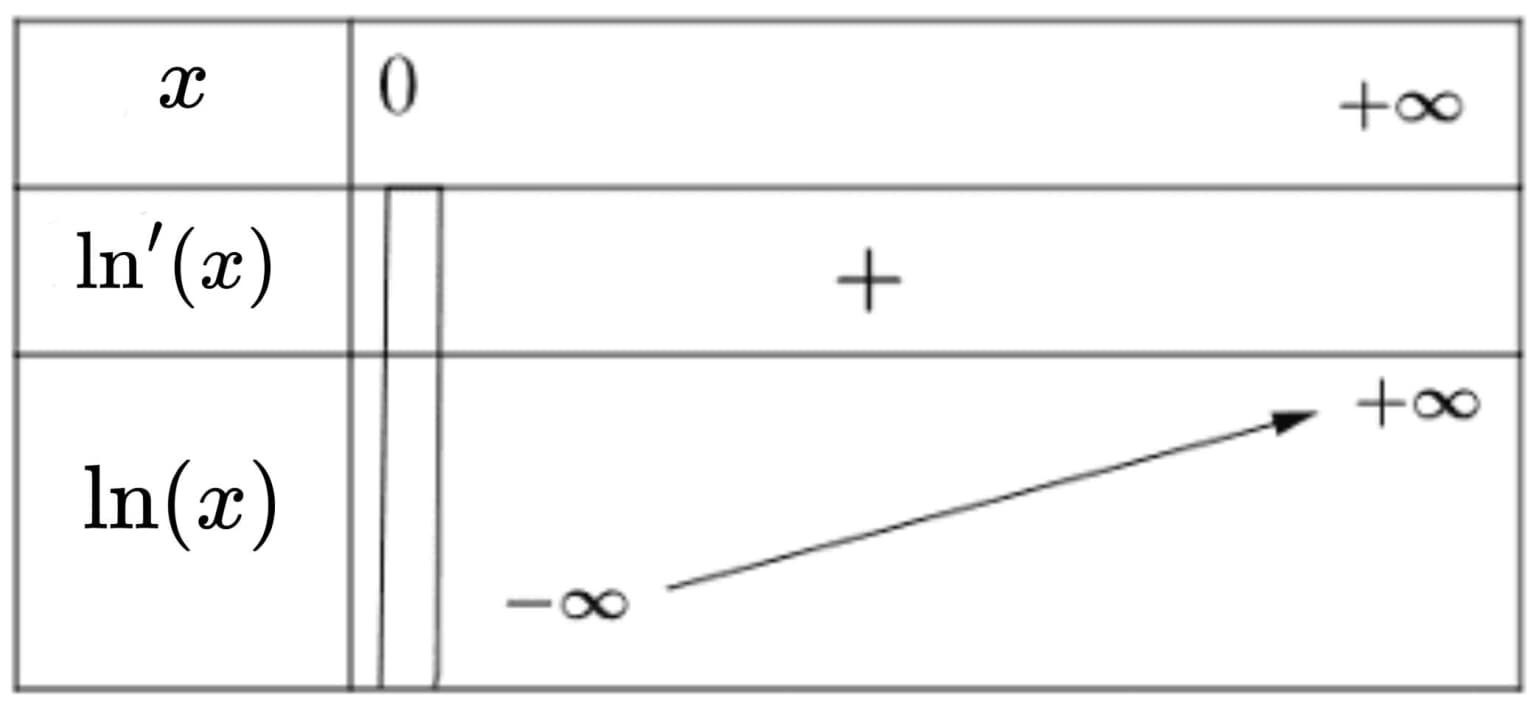
- L'ensemble de définition de la fonction logarithme népérien est $]0~ ; +\infty[$.
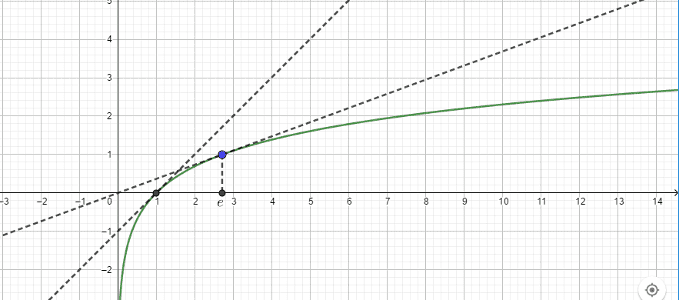
- $\ln 1=0$
- La fonction $\ln$ est dérivable sur $]0~ ;+\infty[$ et sur cet intervalle, sa dérivée est $x \mapsto \dfrac{1}{x}$. Ainsi : pour tout réel $x$ appartenant à $]0~ ;+\infty[$ : $\ln^{\prime}(x)=\dfrac{1}{x}$
Propriétés
- La fonction $\ln$ est continue et strictement croissante sur $\bf{]0~; +\infty[}$.
- Pour tous réels $a$ et $b$ strictement positifs : $\ln a < \ln b \Leftrightarrow a < b$ et $\ln a = \ln b \Leftrightarrow a=b$
Théorème
Soit $u$ une fonction définie, dérivable et strictement positive sur un intervalle $I$.
Alors la fonction $\ln \circ u$ est définie et dérivable sur $\rm I$, et sa fonction dérivée est :
$(\ln \circ u)^{\prime}=\dfrac{u^{\prime}}{u}$
Corollaire
Si une fonction $u$ est dérivable et strictement positive sur un intervalle $\rm I$, alors les primitives de la fonction $\dfrac{u^{\prime}}{u}$ sont les fonctions $\mathrm F_k$ définies sur $\rm I$ par : $\mathrm F_k=(\ln \circ u)+k$, $k$ étant un réel arbitraire.