Fonction exponentielle

Définitions et premières propriétés

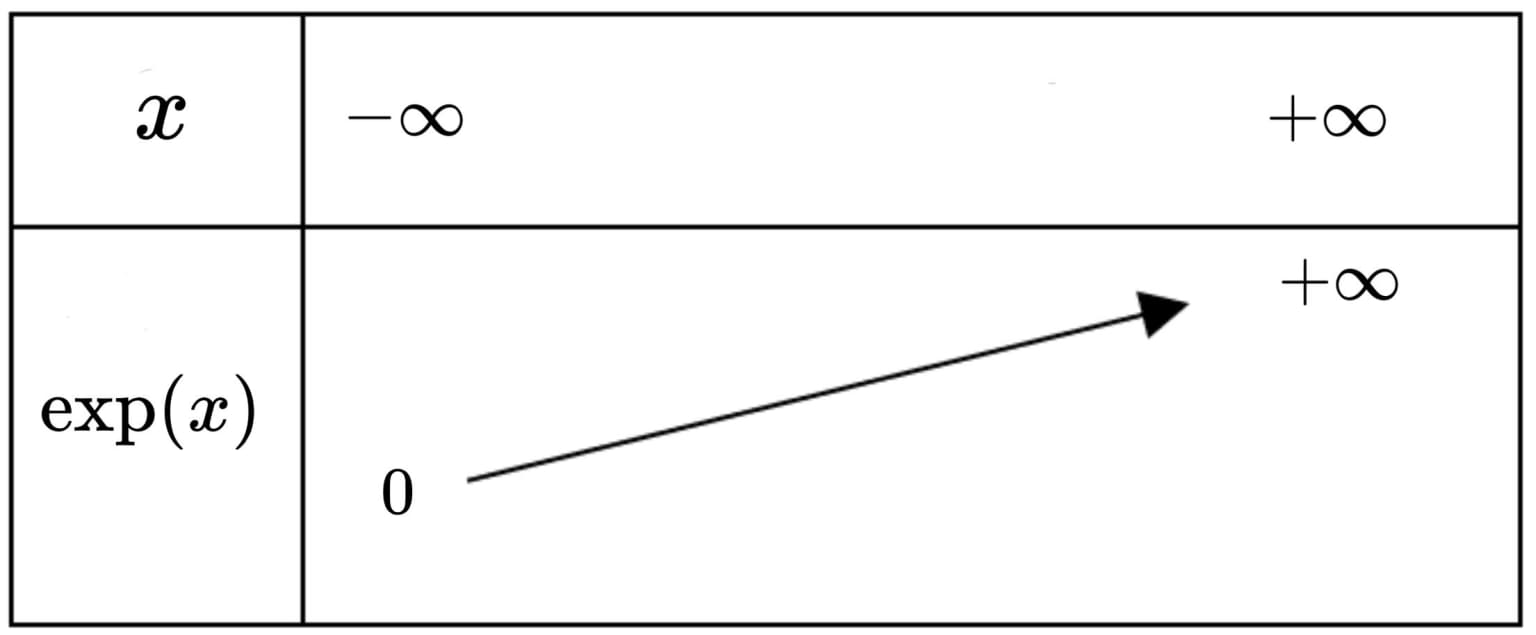
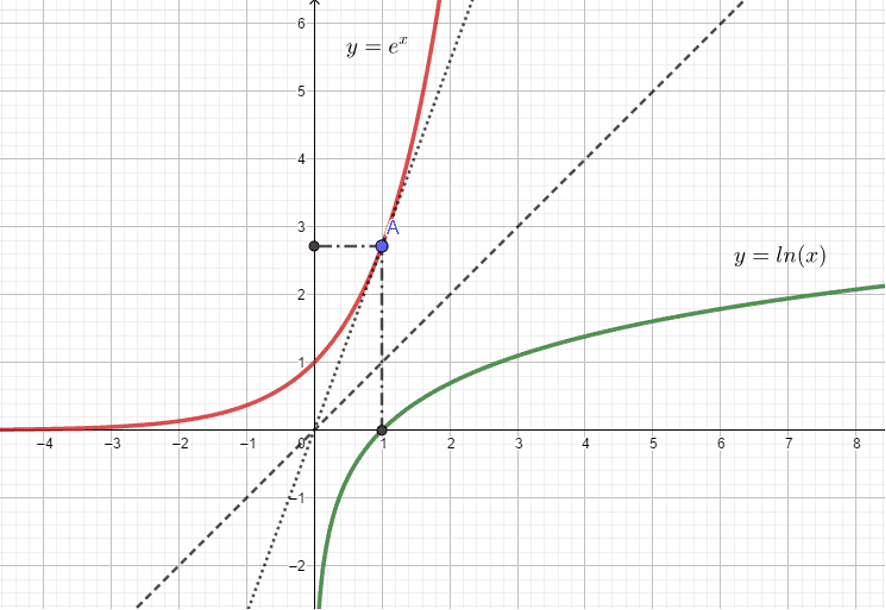
C'est la bijection réciproque de la fonction $\ln$. Elle est définie sur $\mathbb{R}$ et a pour ensemble d'arrivée $]0~ ;+\infty[$. Notons-la provisoirement $\exp$.

Conséquences :

1. Pour tout $x$ appartenant à $\mathbb{R}, \exp x>0$
2. Pour tout $x$ appartenant à $\mathbb{R}$, $\ln (\exp x)=x$
3. Pour tout $x$ appartenant à $]0~ ;+\infty[$, $\exp (\ln x)=x$
4. $\forall(a, b) \in \mathbb{R}^2, \exp a=\exp b \Leftrightarrow a=b$
5. $\exp 0=1$ et $\exp \mathrm{e}=1$ ($\rm e$ étant le réel tel que $\ln \mathrm{e}=1)$
6. Pour tout $n \in \mathbb{Z}$, $\exp n=\mathrm{e}^n$

Nous admettrons que l'on peut prolonger cette dernière notation à tout réel en posant :

Pour tout $x$ appartenant à $\mathbb{R}$
$\exp x=\mathrm{e}^x$

En utilisant cette nouvelle notation, les propriétés suivantes s'écrivent :

Propriétés

1. Pour tout $x$ appartenant à $\mathbb{R}$, $\mathrm{e}^x>0$
2. Pour tout $x$ appartenant à $\mathbb{R}$, $\ln \left(\mathrm{e}^x\right)=x$
3. Pour tout $x$ appartenant à $]0~ ;+\infty[$, $\mathrm{e}^{\ln x}=x$
4. $\forall(a, b) \in \mathbb{R}^2$, $\mathrm{e}^a=\mathrm{e}^b \Leftrightarrow a=b$
5. $\mathrm{e}^0=1$ et $\mathrm{e}^1=\mathrm{e}$

Propriétés algébriques

1. $\forall(a, b) \in \mathbb{R}^2, \mathrm e^{a+b}=\mathrm e^a \times \mathrm e^b$
2. $\forall a \in \mathbb{R}$, $\mathrm e^{2 a}=\left(\mathrm e^a\right)^2$ et plus généralement : $\forall a \in \mathbb{R}$, $\left(\mathrm e^a\right)^n=\mathrm e^{n a}$
3. $\forall a \in \mathbb{R}$, $\mathrm e^{-a}=\dfrac{1}{\mathrm e^a}$
4. $\forall(a, b) \in \mathbb{R}^2$, $\mathrm e^{a-b}=\dfrac{\mathrm e^a}{\mathrm e^b}$

Sens de variation

La fonction exponentielle est strictement croissante sur $\mathbb{R}$. On a donc :

$\forall(a, b) \in \mathbb{R}^2$, $\mathrm e^a < \mathrm e^b \Leftrightarrow a < b$

Continuité et dérivabilité

La fonction exponentielle est dérivable (donc a fortiori continue) sur $\mathbb{R}$ et sa fonction dérivée est la fonction exponentielle.

Autrement dit : pour tout $x$ appartenant à $\mathbb{R}$, $\exp ^{\prime} x=\exp (x)=\mathrm e^x$

Limites remarquables

• $\displaystyle \lim _{x \rightarrow+\infty} \mathrm e^x=+\infty$
• $\displaystyle \lim _{x \rightarrow+\infty} \frac{\mathrm e^x}{x}=+\infty$
• $\displaystyle \lim _{x \rightarrow-\infty} \mathrm e^x=0$
• $\displaystyle \lim _{x \rightarrow-\infty} x \mathrm e^x=0$
• $\displaystyle \lim _{x \rightarrow 0} \frac{\mathrm e^x-1}{x}=1$
• $\displaystyle \lim _{x \rightarrow+\infty} \frac{\mathrm e^x}{x^\alpha}=+\infty$
• $\displaystyle \lim _{x \rightarrow-\infty} x^\alpha \mathrm e^x=0$
  $\alpha$ étant un nombre rationnel strictement positif.

Tableau de variation

Courbe représentative

Noter que la tangente au point $\rm A$ d'abscisse $1$ a pour équation $y=\mathrm{e} x$ ; elle passe donc par l'origine du repère.

Dérivée d'une fonction $\exp \circ u$

Soit $u$ une fonction définie et dérivable sur un intervalle $\rm I$, alors la fonction $\exp \circ u$ est dérivable sur $\rm I$ et I'on a : $(\exp \circ u)^{\prime}=u^{\prime} \times(\exp \circ u)$, ce qui s'écrit aussi $\left(\mathrm{e}^u\right)^{\prime} = u^{\prime} \times\left(\mathrm{e}^u\right)$

Primitives

Soit $u$ une fonction définie et dérivable sur un intervalle $\rm I$. Alors les primitives sur $\mathbb{R}$ de la fonction $u^{\prime} \times\left(\mathrm{e}^u\right)$ sont les fonctions $(\exp \circ u)+k$, $k$ décrivant $\mathbb{R}$.