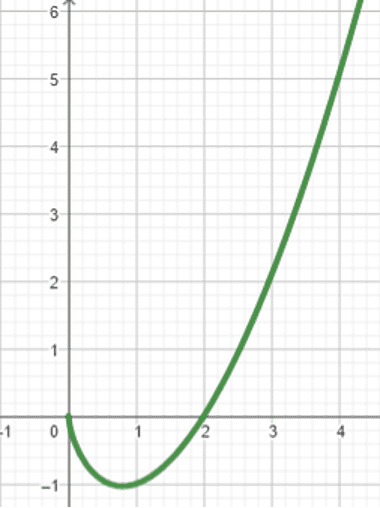
Fonction polynôme
$f: x \mapsto \dfrac{1}{8} x^3+x+4$
La fonction dérivée de $f$ est définie par : $f^{\prime}(x)=\dfrac{3}{8} x^2+1$.
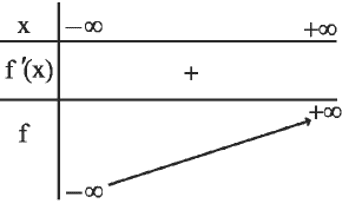
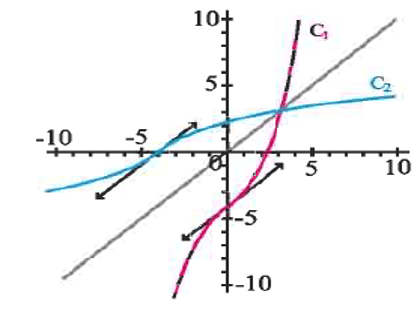
Le lecteur est invité à vérifier que la fonction a le tableau de variation et la courbe ci-dessous. $\mathrm C_2$ désigne la courbe de $f^{-1}$.
Fonction rationnelle
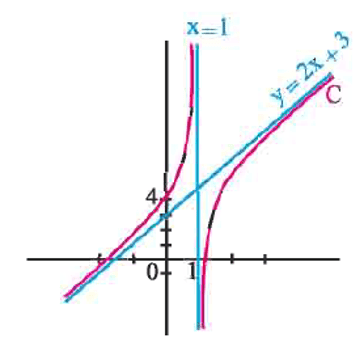
$f: x \mapsto \dfrac{2 x^2+x-4}{x-1}$
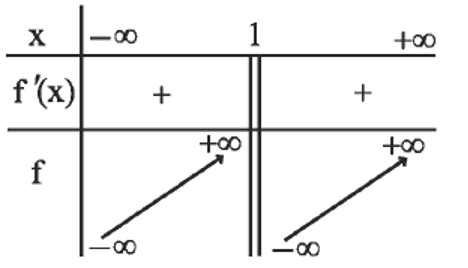
Le lecteur vérifiera que $f(x)$ peut se mettre sous la forme : $2 x+3-\dfrac{1}{x-1}$, que l'expression de la dérivée est $f^{\prime}(x)=2+\dfrac{1}{(x-1)^2}$, et que la fonction a le tableau de variation et la courbe ci-dessous.
Une autre fonction rationnelle
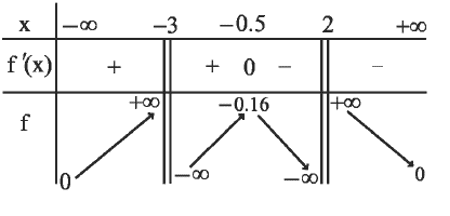
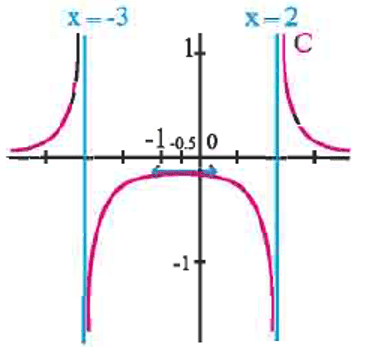
$f: x \mapsto \dfrac{1}{(x+3)(x-2)}$
Le lecteur vérifiera que $f(x)$ peut se mettre sous la forme : $\dfrac{1}{5(x-2)} -\dfrac{1}{5(x+3)^{\prime}}$ que l'expression de la dérivée est $f^{\prime}(x)=\dfrac{-2 x-1}{(x-2)^2(x+3)^2}$, et que la fonction a le tableau de variation et la courbe ci-dessous.
Fonction irrationnelle
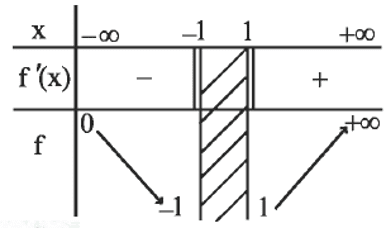
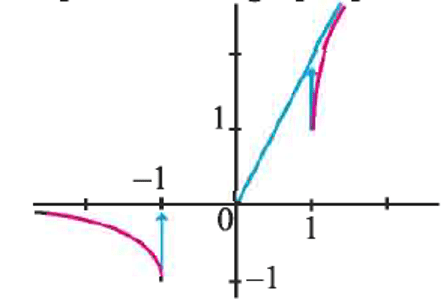
$f: x \mapsto x+\sqrt{x^2-1}$
Le lecteur vérifiera que la droite d'équation $y=2 x$ est asymptote à $\left(\mathrm C_f\right)$ et que l'expression de la dérivée est $f^{\prime}(x)=\dfrac{f(x)}{\sqrt{x^2-1}}$. Le tableau de variation et la courbe ont l'allure ci-dessous.
Fonction trigonométrique
$f: x \mapsto \dfrac{4 \sin x}{2+\cos x}$
Le lecteur vérifiera que $f$ est impaire et périodique de période $2 \pi$.
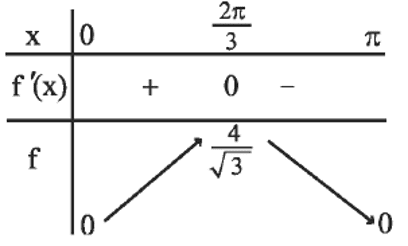
Tableau de variation de $f$ sur $[0~ ; \pi]$
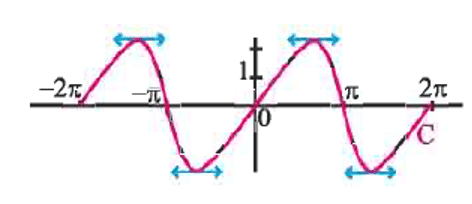
Représentation graphique de $f$ sur $[-2 \pi ~; 2 \pi]$
Fonction puissance
$f: x \mapsto x^{\frac{5}{3}}-2 x^{\frac{2}{3}}$
Le lecteur vérifiera que $f$ a le tableau de variation suivant :
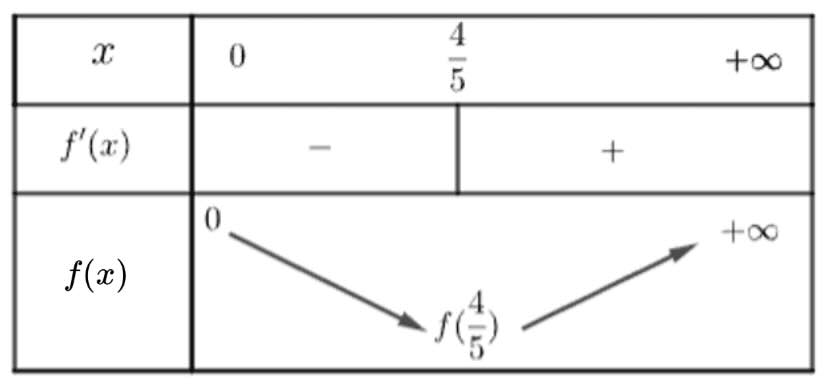
Et que sa courbe a l’allure ci-dessous :