Mouvement d'une particule chargée dans un champ électrique
Définitions du système
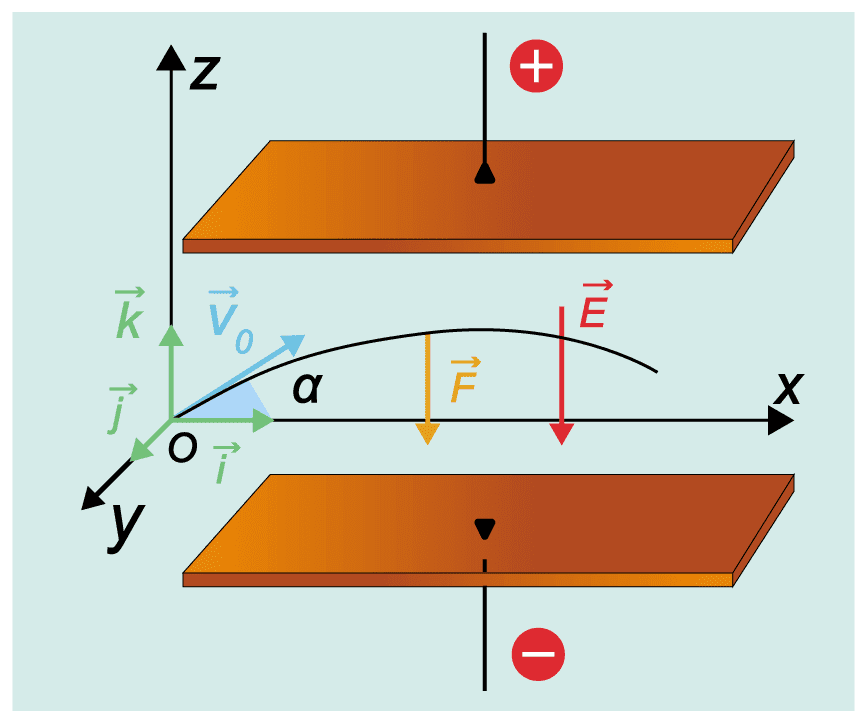
Système : particule de masse $\rm m$ et de charge $q > 0$
Référentiel : terrestre supposé Galiléen
Bilan des forces : Poids négligé
Force électrique et loi de Newton
Force électrique : $\mathrm{F\vec e} = q \times \rm \vec E$
2nde loi de Newton : $\displaystyle \rm \sum \vec F = m\mathcal{\vec a}$ soit $q\rm \vec E = m\mathcal{\vec a}$ et ainsi $\vec a = \dfrac{q}{\rm m}\rm \vec E$.
Équations horaires
Les équations horaires décrivent l'évolution de la vitesse et de la position en fonction du temps.
Vitesse :
$\vec v(t)\left\{\begin{array}{ll} v_x(t) = v_0 \times \cos \alpha\\ v_y(t) = \dfrac{-q\rm E}{\rm m} \times t + v_0 \times \sin \alpha \end{array}\right.$
Position :
$\overrightarrow{\mathrm{OG}(t)}\left\{\begin{array}{lll}\scriptstyle x(t) = v_0 \cos \alpha \times t\\ \scriptstyle y(t) = \frac{1}{2} \times \frac{-q\rm E}{\rm m} \times t^2 + v_0 \times \sin \alpha \times t\end{array}\right.$
Équation de la trajectoire
Pour obtenir l'équation de la trajectoire, on isole $t$ dans $x(t)$ et on remplace dans $y(t)$.
$y(x) = \dfrac{-q\times \rm E}{2\mathrm mv^2_0\cos^2 \alpha} \times x^2 + x \times \tan \alpha$



