Étude du mouvement d'une balle en chute libre
Définition du système et du référentiel
Système : balle de masse $\rm m$
Référentiel : terrestre supposé galiléen
Bilan des forces : poids de la balle
Application de la 2ème loi de Newton
La 2ème loi de Newton s'applique comme suit :
$\displaystyle \rm \sum \overrightarrow{F_{ext}} = m\cdot \overrightarrow{\mathcal{a(t)}}$
$\rm \vec P = m\cdot \overrightarrow{\mathcal{a(t)}}$
$\mathrm m \cdot \vec g = \mathrm m\cdot \overrightarrow{a(t)}$
$\overrightarrow{a(t)} = \vec g = \overrightarrow{\rm cte}$
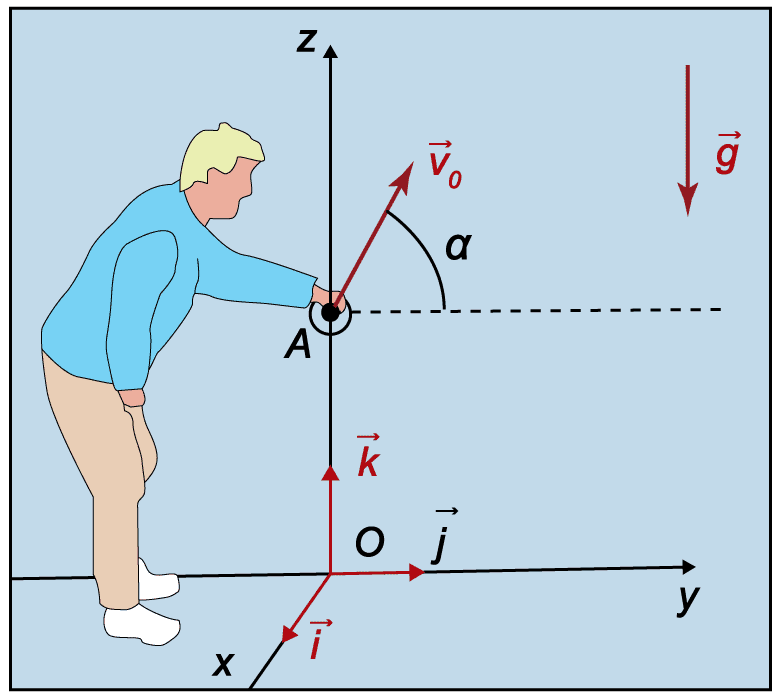
Projection sur les trois axes
On projette les équations du mouvement sur les 3 axes du repère.
Sur Ox -------- $\scriptstyle a_x = 0$ -------- D'où en primitivant : $\scriptstyle v_x = \rm cste_1$
-------- D'où en primitivant : $\scriptstyle x = \mathrm{cste_4} = x(t=0)=0$ d'où $\scriptstyle \boxed{\scriptstyle x(t)=0}$
Sur Oy -------- $\scriptstyle a_y = 0$ -------- D'où en primitivant : $\scriptstyle v_y = \rm cste_2$
-------- D'où en primitivant : $\scriptstyle y = v_0 \times \cos \alpha \times t + \rm cste_5$ d'où $\scriptstyle\boxed{\scriptstyle y(t) = v_0 \times \cos \alpha \times t~~(1)}$
Sur Oz -------- $\scriptstyle a_z = -g$ -------- D'où en primitivant : $\scriptstyle v_z = -g \times t + \rm cste_3$
-------- D'où en primitivant : $\scriptstyle z = -1/2 \times g \times t^2 + v_0 \times \sin \alpha \times t + \rm cste_6$ d'où $\scriptstyle\boxed{\scriptstyle z(t) = -1/2 \times g\times t^2 + v_0 \times \sin \alpha \times t + \rm OA~~(2)}$
Équation de la trajectoire
Grâce à ces deux équations, on peut obtenir l'équation de la trajectoire . L'équation $(1)$ nous donne $t = \dfrac{y}{v_0\times \cos \alpha}$.
On remplace dans $(2)$ : $\scriptstyle\boxed{\scriptstyle x(y) = 1/2 \times g \times \frac{t^2}{v_0^2\times \cos^2 \alpha} + v_0 \times \tan \alpha \times y + \rm OA}$
EN RÉSUMÉ
Pour une balle en chute libre, l'accélération est constante et égale à $\vec{g}$. La projection sur les axes donne des équations horaires permettant de déterminer la trajectoire du projectile en fonction des conditions initiales.