Description d’un mouvement

Le référentiel en physique

Un référentiel est un solide (un ensemble de points fixes entre eux) par rapport auquel on repère une position ou un mouvement.

Composants d'un référentiel

À chaque référentiel est associé :

• un repère d'espace pour quantifier la position ;
• un repère de temps (une horloge) pour associer une date à chaque position.

Vecteur-position

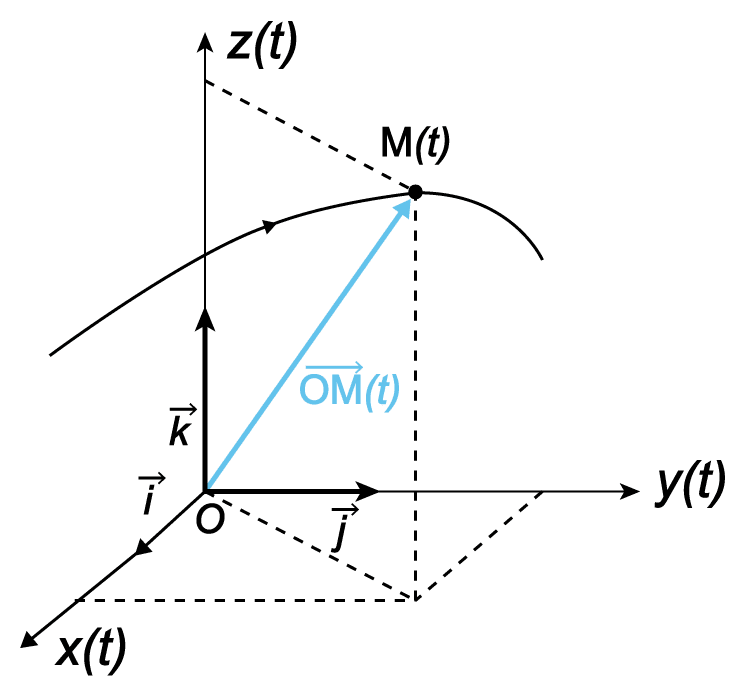
La position d'un mobile $\rm M$ dans un repère $(\mathrm O, \vec i, \vec j, \vec k)$ est donné par son vecteur-position $\rm \overrightarrow{OM}$ :

$\overrightarrow{\rm OM} (t)\begin{pmatrix}x(t)\\y(t)\\z(t)\end{pmatrix}$ $\Leftrightarrow$ $\overrightarrow{\rm OM}(t) = x(t) \vec i + y(t) \vec j + z(t) \vec k$

Trajectoire d'un mobile

L'ensemble des points est occupé successivement par le mobile $\rm M$ au cours du temps appelé trajectoire.

La trajectoire d'un point correspond à l'ensemble des positions successives occupées par ce point au cours de son mouvement.

Le vecteur-vitesse

Le vecteur-vitesse $\vec v(t)$ caractérise la variation du vecteur-position en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur position.

Expression du vecteur-vitesse instantanée

Le vecteur-vitesse instantanée au point $\mathrm M_i$ s'écrit donc :

$$\boxed{\overrightarrow{v(t)} = \frac{\rm d\overrightarrow{OM}}{\mathrm dt}} \left\{\begin{array}{ll}t \text{ en s}\\ \rm OM \text{ en m}\\ v \text{ en } \rm m.s^{-1}\end{array}\right.$$

Composantes du vecteur-vitesse

$\vec v(t) = v_x(t) \vec i + v_y (t) \vec j + v_z(t)\vec k$ avec $\vec v \left|\begin{array}{lll}v_x = \dfrac{\mathrm dx}{\mathrm dt}\\v_y = \dfrac{\mathrm dy}{\mathrm dt}\\v_z = \dfrac{\mathrm dz}{\mathrm dt}\end{array}\right.$

Caractéristiques du vecteur-vitesse

Les caractéristiques du vecteur-vitesse sont les suivantes :

$$\vec v(t)\left\{\begin{array}{lll}\scriptstyle \text{direction : tangent à la trajectoire}\\ \scriptstyle\text{sens : celui du mouvement}\\ \scriptstyle\text{valeur (norme) : } \|\vec v\| = v = \sqrt{v_x^2+v_y^2+v_z^2}\end{array}\right.$$

Le vecteur-accélération

Le vecteur-accélération $\vec a (t)$ caractérise la variation du vecteur-vitesse en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur position.

Expression mathématique

Le vecteur-accélération au point $\mathrm M_i$ s'écrit donc :

$$\boxed{\overrightarrow{a(t)} = \frac{\mathrm d\vec v}{\mathrm dt} = \frac{\rm d^2\overrightarrow{OM}}{\mathrm dt^2}} \left\{\begin{array}{ll}t \text{ en s}\\ v \text{ en } \rm m.s^{-1}\\ a \text{ en } \rm m.s^{-2}\end{array}\right.$$

Composantes du vecteur-accélération

Le vecteur-accélération peut être décomposé selon les trois axes de l'espace :

$$\vec a(t) = a_x(t) \vec i + a_y (t) \vec j + a_z(t)\vec k$$

avec $$\vec a \left|\begin{array}{lll}a_x = \dfrac{\mathrm dv_x}{\mathrm dt} = \dfrac{\mathrm d^2x}{\mathrm dt^2}\\a_y = \dfrac{\mathrm dv_y}{\mathrm dt} = \dfrac{\mathrm d^2y}{\mathrm dt^2}\\a_z = \dfrac{\mathrm dv_z}{\mathrm dt} = \dfrac{\mathrm d^2z}{\mathrm dt^2}\end{array}\right.$$

Caractéristiques du vecteur-accélération

Les caractéristiques du vecteur-accélération sont les suivantes :

$$\vec a(t)\left\{\begin{array}{lll}\scriptstyle \text{direction : celle du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{sens : celui du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{valeur (norme) : } a = \frac{\Delta v}{\Delta t} = \|\vec a\| = \sqrt{a_x^2+a_y^2+a_z^2}\end{array}\right.$$

Mouvements rectilignes

Repère de Frenet

$\vec a = a_{\rm T}\overrightarrow{u_{\rm T}} + a_{\rm N}\overrightarrow{u_{\rm N}}$ avec $\boxed{a_{\rm T} = \dfrac{\mathrm dv}{\mathrm dt}}$ et $\boxed{a_{\rm N} = \left(\dfrac{v^2}{\rm R}\right)}$

L'accélération tangentielle $a_{\rm T}$ caractérise la variation de la valeur de la vitesse, tandis que l'accélération normale $a_{\rm N}$ caractérise le changement de direction du vecteur vitesse.

Mouvements circulaires

Deuxième loi de Newton

Dans un référentiel Galiléen $\boxed{\displaystyle \sum \mathrm{\vec F_{ext}} = \mathrm m\dfrac{\mathrm d\vec v}{\mathrm dt}= \mathrm m\vec a}$

Rappel : Première loi de Newton

« Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme si les forces qui s'exercent sur lui se compensent ».

$\displaystyle \vec F_{ext} = \vec 0$