Fonctions trigonométriques

Valeurs remarquables

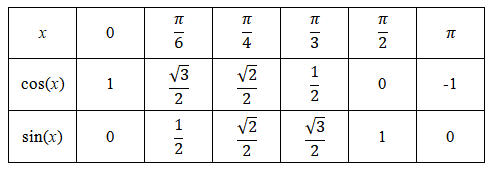
Cosinus et sinus d'angles associés

Formules pour le cosinus

Pour tout nombre réel $x$ :

• $\cos(-x) = \cos(x)$  
• $\displaystyle \cos(x + \frac{\pi}{2}) = -\sin(x)$  
• $\cos(x + \pi) = -\cos(x)$  
• $\displaystyle \cos(x - \frac{\pi}{2}) = \sin(x)$  

Formules pour le sinus

Pour tout nombre réel $x$ :

• $\sin(-x) = -\sin(x)$  
• $\displaystyle \sin(x + \frac{\pi}{2}) = \cos(x)$  
• $\sin(x + \pi) = -\sin(x)$  
• $\displaystyle \sin(x - \frac{\pi}{2}) = -\cos(x)$  

Les fonctions trigonométriques

Fonction cosinus

La fonction cosinus est définie sur $\mathbb{R}$. Elle est périodique de période $2\pi$ et sa représentation graphique (en bleu) est une sinusoïde de période $2\pi$. La fonction cosinus est paire donc sa représentation graphique est symétrique par rapport à l'axe des ordonnées.

Fonction sinus

La fonction sinus est définie sur $\mathbb{R}$. Elle est périodique de période $2\pi$ et sa représentation graphique (en noir) est une sinusoïde de période $2\pi$. La fonction sinus est impaire donc sa représentation graphique est symétrique par rapport à l'origine du repère.