Droites du plan

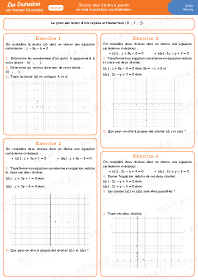
Équations de droites dans le plan

On munit le plan d'un repère orthonormal $(\mathrm O~ ; \vec{i}~ ; \vec{j})$.

Équation réduite de droite

Il existe deux types d'équations selon l'orientation de la droite :

• Une droite verticale a pour équation $x = a$ avec $a$ un nombre réel.
• Si une droite n'est pas verticale, elle a pour équation $y = f(x) = ax + b$ avec $a$ et $b$ deux nombres réels. $a$ est le coefficient directeur de cette droite et $b$ son ordonnée à l'origine.

Calcul du coefficient directeur

Si les points $\mathrm A(x_{\mathrm{A}} ; y_{\mathrm{A}})$ et $\mathrm B(x_{\mathrm{B}} ; y_{\mathrm{B}})$ appartiennent à cette droite non verticale, le coefficient directeur de cette droite est égal à :

$$a = \frac{y_{\mathrm{B}} - y_{\mathrm{A}}}{x_{\mathrm{B}} - x_{\mathrm{A}}}$$

Droites parallèles

Deux droites non verticales sont parallèles si et seulement si elles ont même coefficient directeur.

Droites perpendiculaires

Deux droites non verticales sont perpendiculaires si et seulement si le produit de leur coefficient directeur est égal à $-1$.

Système de deux équations à deux inconnues

Pour résoudre un système de deux équations à deux inconnues du premier degré, il faut trouver le ou les couples $(x ; y)$ qui sont solutions simultanément des deux équations. Les deux méthodes de résolution sont celle par combinaison et celle par substitution.

Objectif de la résolution

L'objectif est de déterminer les valeurs de $x$ et $y$ qui vérifient les deux équations en même temps. Ces valeurs forment un couple solution $(x ; y)$.

Méthodes de résolution

Il existe deux principales méthodes pour résoudre ce type de système :

• Méthode par combinaison : Elle consiste à éliminer une inconnue en combinant les deux équations
• Méthode par substitution : Elle consiste à exprimer une inconnue en fonction de l'autre dans une équation, puis à la substituer dans la seconde équation