Structure
La structure union-find, ou DSU (Disjoint Set Union), est une structure de données efficace pour gérer un ensemble de sous-ensembles disjoints. Elle est utilisée dans des problèmes liés à la connectivité, comme déterminer si deux éléments appartiennent à une même classe d'équivalence.
Ses principales opérations sont :
- find(x) : détermine le représentant (racine) de la classe d'équivalence contenant x.
- union(x, y) : fusionne les classes d'équivalence contenant x et y.
- makeSet() : initialise un singleton pour chaque élément distinct, étape préalable à l'utilisation de la structure.
Implémentation
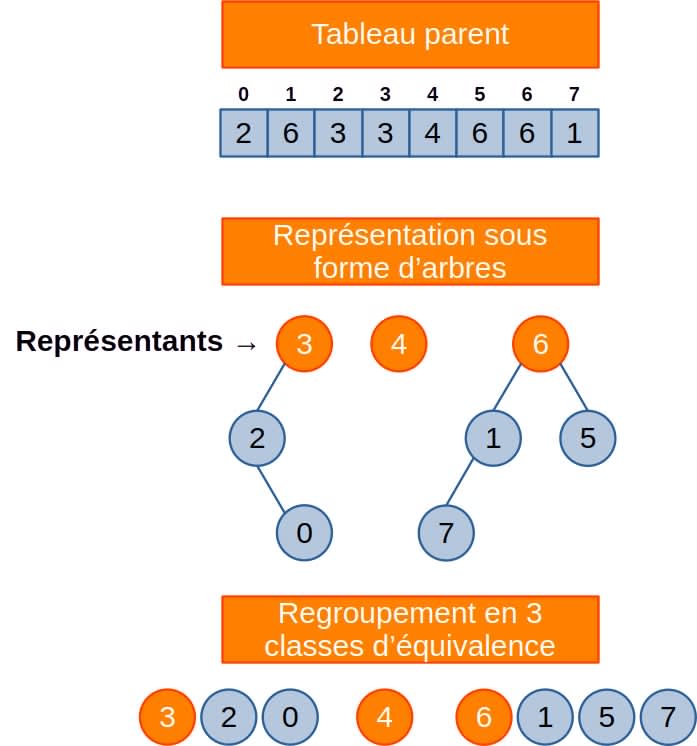
Une implémentation courante repose sur une représentation sous forme d'arbre. Chaque classe d'équivalence est représentée par un arbre dont le représentant est la racine.
Cette structure peut être implémentée avec un simple tableau dans lequel chaque élément (représenté par les indices) pointe vers son parent, ou vers lui-même s'il est une racine.
Optimisation
Union par rang
Un tableau de rang peut être ajouté à la structure. Ce tableau stocke une borne supérieure de la profondeur potentielle de l'arbre, uniquement pour les représentants (racines). Lors d'une union, il est utilisé pour attacher l'arbre de rang inférieur sous la racine de l'arbre de rang supérieur, équilibrant ainsi les arbres et accélérant les opérations suivantes.
Compression de chemin
La compression de chemin est une stratégie permettant d'optimiser les opérations find(x). Elle consiste à connecter directement tous les nœuds rencontrés sur le chemin de recherche à la racine, réduisant ainsi la profondeur des arbres.
Complexité
Dans sa version de base, sans optimisation, une opération individuelle peut coûter jusqu'à $O(n)$, ce qui conduit à une complexité totale de $O(n)$ pour une série de n opérations.
Avec union par rang, la complexité amortie passe à $O(\log n)$.
Avec compression de chemin, combinée à l'union par rang, la complexité amortie atteint $O(\alpha(n))$ où $\alpha$ (fonction d'Ackermann) croît extrêmement lentement, rendant les opérations presque constantes dans la pratique.


