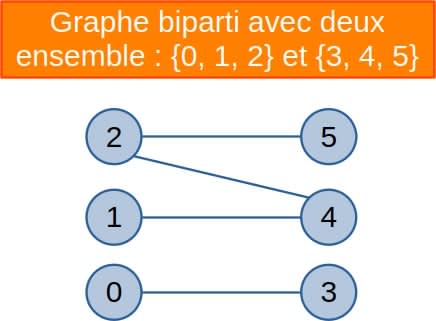
Graphe biparti
Un graphe biparti est un graphe dont les sommets peuvent être divisés en deux ensembles disjoints $U$ et $V$ tels que chaque arête relie un sommet de $U$ à un sommet de $V$.
Aucun sommet n'est relié à un sommet du même ensemble.
Couplage
Un couplage dans un graphe est un ensemble d'arêtes tel qu'aucun sommet n'est incident à plus d'une arête du couplage. Chaque sommet appartient au plus à une seule paire dans le couplage.
Des sommets reliés par une arête du couplage sont dits couplés ou appairés, tandis que les autres sommets sont dits libres.
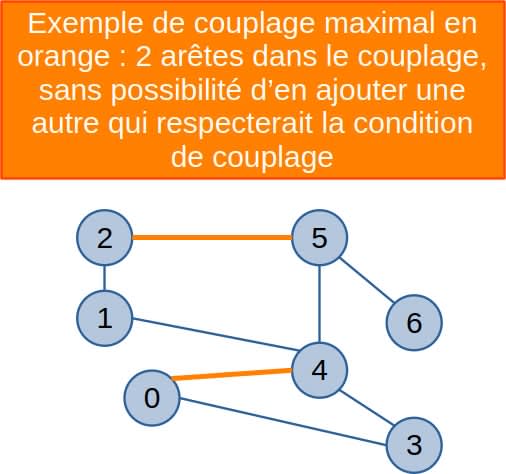
Couplage maximal
Un couplage maximal est un couplage qui ne peut pas être étendu en ajoutant une arête supplémentaire. Aucune arête ne pourrait être ajoutée au couplage sans violer la propriété qu'aucun sommet ne doit être incident à plus d'une arête.
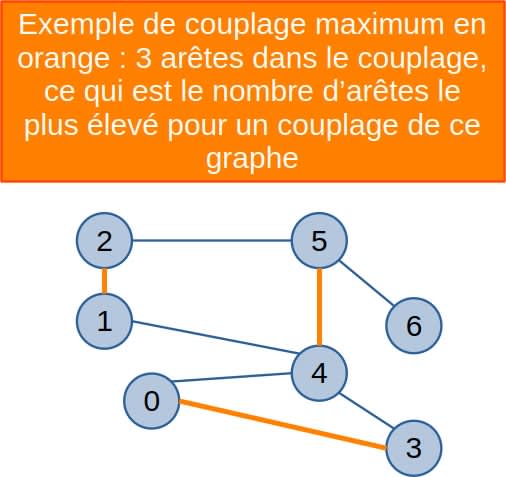
Couplage maximum
Un couplage de cardinal maximum est un couplage qui contient le plus grand nombre possible d'arêtes pour un graphe donné.
Un graphe peut admettre plusieurs couplages maximums différents.
Couplage parfait
Un couplage parfait est un couplage où tous les sommets du graphe sont appairés. Chaque sommet est incident à exactement une arête du couplage.
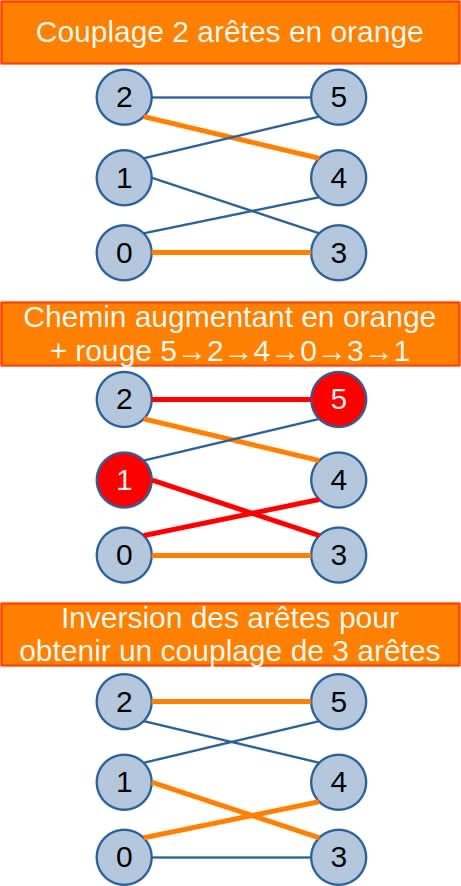
Chemin augmentant
Un chemin augmentant est un chemin alternant entre des arêtes qui appartiennent au couplage actuel et des arêtes qui n'y appartiennent pas, en commençant et en terminant par des sommets libres (non appairés).
L'utilisation de ces chemins est centrale pour améliorer un couplage et déterminer un couplage maximum. En effet, en inversant les arêtes sur un chemin augmentant (c'est-à-dire en remplaçant les arêtes du couplage par des arêtes hors du couplage, et vice versa), on obtient un nouveau couplage contenant une arête de plus.
Dans un graphe biparti, la recherche d'un chemin augmentant permet de résoudre des problèmes d'allocation optimale, comme l'assignation de tâches à des travailleurs ou de projets à des étudiants.