Grammaire non contextuelle – Dérivation et arbre d’analyse

Grammaire formelle

Une grammaire formelle est un ensemble de règles permettant de générer tous les mots (ou chaînes) valides d'un langage donné. Elle est définie comme un quadruplet $G = (V, \Sigma, P, S)$, où :

• $V$ est un ensemble fini de symboles non terminaux (ou variables) ;
• $\Sigma$ est un ensemble fini de symboles terminaux, disjoints de $V$, représentant les éléments du langage ;
• $P$ est un ensemble fini de règles de production de la forme $A \to \gamma$, où $A \in V$ et $\gamma \in (V \cup \Sigma)^*$ ;
• $S$ sert de symbole de départ ($S \in V$).

Grammaire non contextuelle

Une grammaire est dite non contextuelle si toutes ses règles de production respectent la forme $A \to \gamma$ où :

• $A \in V$ est un unique terme non-terminal, à gauche de la règle ;
• $\gamma \in (V \cup \Sigma)^*$ est une combinaison quelconque de terminaux et non-terminaux, à droite de la règle de production.

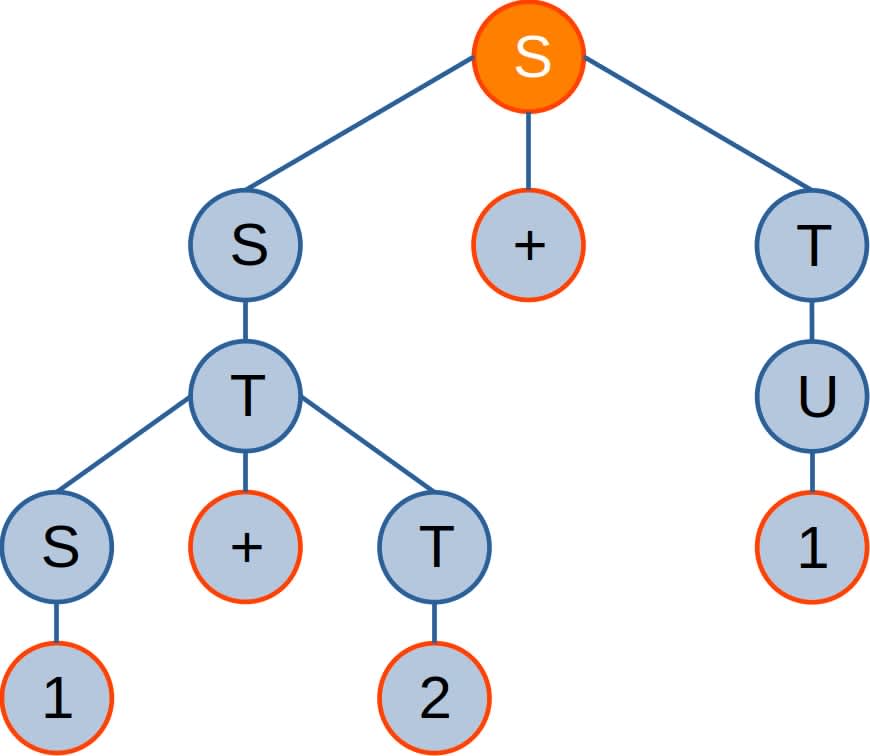
Le langage engendré par une grammaire non contextuelle est l'ensemble des mots pouvant être formés uniquement de symboles terminaux, et qui peuvent être dérivées à partir du symbole initial S en appliquant les règles de production.

Langage de programmation

Les grammaires non contextuelles sont fondamentales pour les langages de programmation, car elles permettent d'analyser les structures syntaxiques complexes des programmes (par exemple, les expressions arithmétiques imbriquées, les blocs de code, etc.).

Grammaire contextuelle

Les grammaires non contextuelles tirent leur nom du fait que les règles de production ne dépendent pas du contexte dans lequel apparaît le symbole à remplacer : cela correspond au fait que symbole à gauche de la règle de production est seul, donc sans contexte.

Cela les différencie des grammaires dites contextuelles ou le symbole de gauche doit être contextualisé, avec d'autres symboles qui peuvent l'accompagner, dans les règles de production.

Dérivation 

Dérivation immédiate

Une dérivation immédiate consiste à appliquer une seule règle de production pour remplacer un non-terminal par une séquence de symboles. Par exemple, à partir de $S$, si l'on applique la règle $S → S + T$, on obtient une dérivation immédiate qu'on note $S \Rightarrow S + T$.

Dérivation

Un mot est obtenu après une série de dérivations immédiates qui aboutissent à ne plus avoir de symboles non terminaux dans l'expression. Si à partir de $S$ on peut produire le mot $1 + 2 + 1$ après une série de dérivations immédiates, on notera $S \Rightarrow^* 1 + 2 + 1$ et on dira que $S$ dérive en $1 + 2 + 1$.

Ambiguïté d'une grammaire

Une grammaire est ambiguë si une chaîne terminale peut être dérivée de plusieurs manières différentes. Cela se traduit par plusieurs arbres de dérivation possibles.

Dérivation à gauche et à droite

La dérivation à gauche consiste, à chaque étape / dérivation, à remplacer le non-terminal le plus à gauche de l'expression jusqu'à obtenir un mot.

La dérivation à droite consiste, à chaque étape / dérivation, à remplacer le non-terminal le plus à droite de l'expression jusqu'à obtenir un mot.

Exemple

Considérons la grammaire $G = (V, \Sigma, P, S)$ avec :

• $V = \{S\}$
• $\Sigma = \{1, 2, +\}$
• $P = \{S \to S + T | T, T \to U | U + V, U \to V | 1, V \to 2 \}$
• $S = S$

Par dérivation à gauche, on peut construire $1 + 2 + 1$ de la manière suivante : $S \Rightarrow S + T \Rightarrow T + T \Rightarrow U + V + T \Rightarrow 1 + V + T \Rightarrow 1 + 2 + T \Rightarrow 1 + 2 + 1$

Par dérivation à droite, on peut construire le mot $1 + 2 + 1$ de la manière suivante : $S \Rightarrow S + T \Rightarrow S + U \Rightarrow S + 1 \Rightarrow T + 1 \Rightarrow U + V + 1 \Rightarrow U + 2 + 1 \Rightarrow 1 + 2 + 1$

Arbre d'analyse

Un arbre d'analyse (ou arbre de dérivation) est une représentation hiérarchique de la manière dont un mot est produit par une grammaire. Chaque nœud correspond à un symbole non-terminal, et chaque feuille à un symbole terminal. Les enfants d'un nœud correspondent aux composants de la règle de production appliquée.

Le mot produit est obtenu en lisant toutes les feuilles de l'arbre de gauche à droite.

Exemple

On reprend la grammaire présentée ci-dessus, avec l'expression $1 + 2 + 1$ construite par dérivation à gauche. L'arbre d'analyse équivalent à cette dérivation est :