Déduction naturelle – Règles d’introduction et d’élimination

Déduction naturelle

La déduction naturelle modélise le raisonnement logique à travers des prémisses, des règles d'inférence, et des dérivations.

Les prémisses sont les hypothèses de départ. Une dérivation consiste à utiliser ces prémisses pour justifier une conclusion.

Un séquent est une expression de la forme $H_1, H_2, \dots, H_n \vdash C$, où $H_1, \dots, H_n$ (les prémisses) permettent de déduire $C$ (la conclusion).

Le symbole $\vdash$ se lit comme « implique logiquement ». Par exemple, $p, p \to q \vdash q$ signifie que $q$ est déductible de $p$ et $p \to q$.

Exemples de règles d'inférence

Modus ponens

$$\frac{p \to q, \, p}{q}$$

Illustration :
Prémisses : "Si la température est négative, l'eau gèle" ($p \to q$) et "La température est négative" ($p$).
Conclusion : "L'eau gèle" ($q$).

Modus tollens

$$\frac{p \to q, \, \neg q}{\neg p}$$

Illustration :
- Prémisses : "Si la température est négative" ($p \to q$) et "L'eau ne gèle pas" ($\neg q$).
- Conclusion : "L'eau ne gèle pas" ($\neg p$).

Syllogisme Barbara

$$\frac{A \to B, \, B \to C}{A \to C}$$

Illustration :
- Prémisses : "Tous les chiens sont des mammifères" ($A \to B$) et "Tous les mammifères sont des vertébrés" ($B \to C$).
- Conclusion : "Tous les chiens sont des vertébrés" ($A \to C$).

Arbres de preuve

Un arbre de preuve organise les relations entre prémisses, règles d'inférence, et conclusions sous forme hiérarchique. C'est une aide à l'organisation d'une démonstration.

Exemple avec des phrases

Hypothèse 1 : "Si la température est négative, l'eau gèle"
Hypothèse 2 : "La température est négative"
Hypothèse 3 : "Si l'eau gèle, conduire est dangereux"

Conclusion : "Conduire est dangereux"

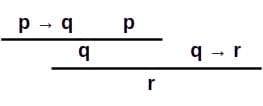
Exemple avec des symboles

Introduction et élimination

Une règle d'introduction spécifie comment on peut prouver une formule contenant un connecteur logique donné. En d'autres termes, elle indique dans quelles conditions une conclusion contenant ce connecteur est valide.

Une règle d'élimination spécifie comment utiliser une formule contenant un connecteur logique pour en déduire une nouvelle conclusion. Elle exploite l'information déjà contenue dans une formule.

Conjonction ($\land$)

Règle d'introduction

$$\frac{\Gamma \vdash p \quad \Gamma \vdash q}{\Gamma \vdash p \land q} \quad (\text{Conjonction introduite si les deux sont prouvées.})$$

Si $p$ et $q$ sont prouvées, on peut conclure $p \land q$.

Règle d'élimination (gauche)

$$\frac{\Gamma \vdash p \land q}{\Gamma \vdash p} \quad (\text{On extrait $p$ de $p \land q$.})$$

Si $p \land q$ est prouvée, on peut conclure $p$.

Règle d'élimination (droite)

$$\frac{\Gamma \vdash p \land q}{\Gamma \vdash q} \quad (\text{On extrait $q$ de $p \land q$.})$$

Si $p \land q$ est prouvée, on peut conclure $q$.

Disjonction ($\lor$)

Règle d'introduction (gauche)

$$\frac{\Gamma \vdash p}{\Gamma \vdash p \lor q} \quad (\text{On introduit $\lor$ en supposant $p$.})$$

Si $p$ est prouvée, on peut conclure $p \lor q$.

Règle d'introduction (droite)

$$\frac{\Gamma \vdash q}{\Gamma \vdash p \lor q} \quad (\text{On introduit $\lor$ en supposant $q$.})$$

Si $q$ est prouvée, on peut conclure $p \lor q$.

Règle d'élimination (preuve par cas) :

$$\frac{\Gamma \vdash p \lor q \quad \{\Gamma, p \vdash r\} \quad \{\Gamma, q \vdash r\}}{\Gamma \vdash r} \quad (\text{Élimination de $\lor$ : on prouve $r$ à partir de $p \lor q$.})$$

Si $p \lor q$ est prouvée et que $r$ est prouvée séparément à partir de $p$ et de $q$, alors $r$ est vrai.

Négation ($\neg$)

Règle d'introduction

$$\frac{\{\Gamma, p \vdash \bot\}}{\Gamma \vdash \neg p} \quad (\text{Si $p$ conduit à une contradiction, on prouve $\neg p$.})$$

Si $p$ implique $\bot$, on peut conclure $\neg p$.

Règle d'élimination

$$\frac{\Gamma \vdash \neg p \quad \Gamma \vdash p}{\Gamma \vdash \bot} \quad (\text{Une contradiction est prouvée si $p$ et $\neg p$ sont toutes deux prouvées.})$$

Si $\neg p$ et $p$ sont toutes les deux prouvées, on obtient une contradiction $\bot$.

Implication ($\to$)

Règle d'introduction

$$\frac{\{\Gamma, p \vdash q\}}{\Gamma \vdash p \to q} \quad (\text{Si $q$ peut être prouvée en supposant $p$, on prouve $p \to q$.})$$

Si $p$ implique $q$, on peut conclure $p \to q$.

Règle d'élimination (modus ponens)

$$\frac{\Gamma \vdash p \to q \quad \Gamma \vdash p}{\Gamma \vdash q} \quad (\text{Modus ponens : si $p \to q$ et $p$ sont prouvées, $q$ l'est aussi.})$$

Si $p \to q$ et $p$ sont prouvées, on peut conclure $q$.

Contradiction ($\bot$)

Élimination de $\bot$ (principe d'explosion)

$$\frac{\Gamma \vdash \bot}{\Gamma \vdash p} \quad (\text{De $\bot$, on peut conclure n'importe quoi.})$$

Si $\bot$ est prouvée, tout est logiquement vrai dans ce contexte.