Automate fini déterministe/non-déterministe – Automate, expression régulière et langage

Définition

Un automate fini déterministe (AFD) $\mathcal{A}$ est défini comme un quintuplet $(\Sigma, Q, \delta, q_0, F)$ où :

• $\Sigma$ est un alphabet fini de symboles ;
• $Q$ est un ensemble fini d'états ;
• $\delta : Q \times \Sigma \to Q$ est une fonction de transition ;
• $q_0 \in Q$ est l'état initial ;
• $F \subseteq Q$ est un ensemble d'états finaux ou acceptants.

La reconnaissance d'un mot $w = a_1a_2\ldots a_n \in \Sigma^*$ par l'automate se fait en déterminant si une suite d'applications de $\delta$ depuis $q_0$ aboutit à un état de $F$.

Notions associées

État initial : L'état $q_0$ à partir duquel commence toute exécution de l'automate.

État final : Un état $q \in F$ où l'automate accepte un mot.

Transition : Une relation définie par $\delta(q, a) = q'$, représentant un passage de l'état $q$ à $q'$ par la lecture du symbole $a$.

Chemin : Une séquence d'états $q_0, q_1, \ldots, q_n$ telle que pour chaque $i$, il existe une transition $\delta(q_i, a_{i+1}) = q_{i+1}$.

État accessible : Un état $q \in Q$ tel qu'il existe un chemin de $q_0$ à $q$.

État co-accessible : Un état $q \in Q$ tel qu'il existe un chemin de $q$ à un état final.

État puits : État dans lequel l'automate peut entrer, mais une fois qu'il y est, il ne peut pas en sortir. Aucun mot reconnu par l'automate ne peut y être validé.

Graphe émondé : Le graphe obtenu en retirant tous les états qui ne sont ni accessibles ni co-accessibles.

Langage reconnu : L'ensemble des mots $L \subseteq \Sigma^*$ tels que $\hat{\delta}(q_0, w) \in F$.

Exemple

Soit un automate $\mathcal{A}$ défini par :

• un alphabet $\Sigma = \{a, b\}$ ;
• un ensemble d'état $Q = \{q_0, q_1, q_2, q_3\}$ ;
• une fonction de transition $\delta : Q \times \Sigma \to Q$, définie par :

$$ \begin{aligned} \delta(q_0, a) &= q_1, \\ \delta(q_0, b) &= q_1, \\ \delta(q_1, b) &= q_2, \\ \delta(q_1, a) &= q_3, \\ \delta(q_2, a) &= q_2. \end{aligned} $$

• un état initial $q_0 \in Q$, représenté par la flèche d'entrée dans l'automate ;
• un état final $q_2 \in Q$, représenté par l'état avec une bordure double.

Voici sa représentation graphique :

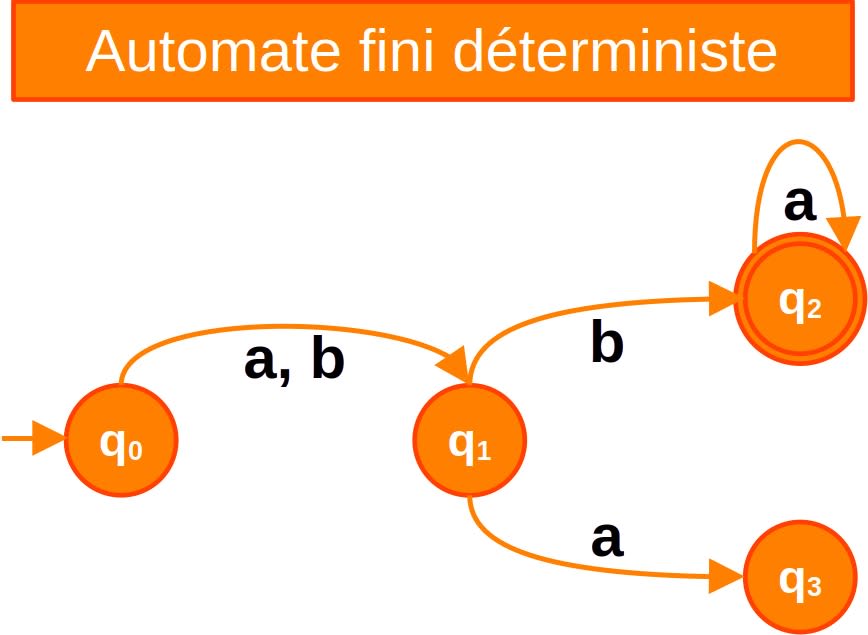
Cet automate reconnaît par exemple les mots :

• ab en passant de l'état $q_0$ à $q_1$ avec la transition a, et de $q_1$ à $q_2$ avec la transition b ;
• bbaa en passant de l'état $q_0$ à $q_1$ avec la transition b, de $q_1$ à $q_2$ avec la transition b, puis en bouclant deux fois sur $q_2$ avec la transition a.

Les mots aa ou abba ne sont en revanche pas reconnus par cet automate et ne font pas partie de son langage.

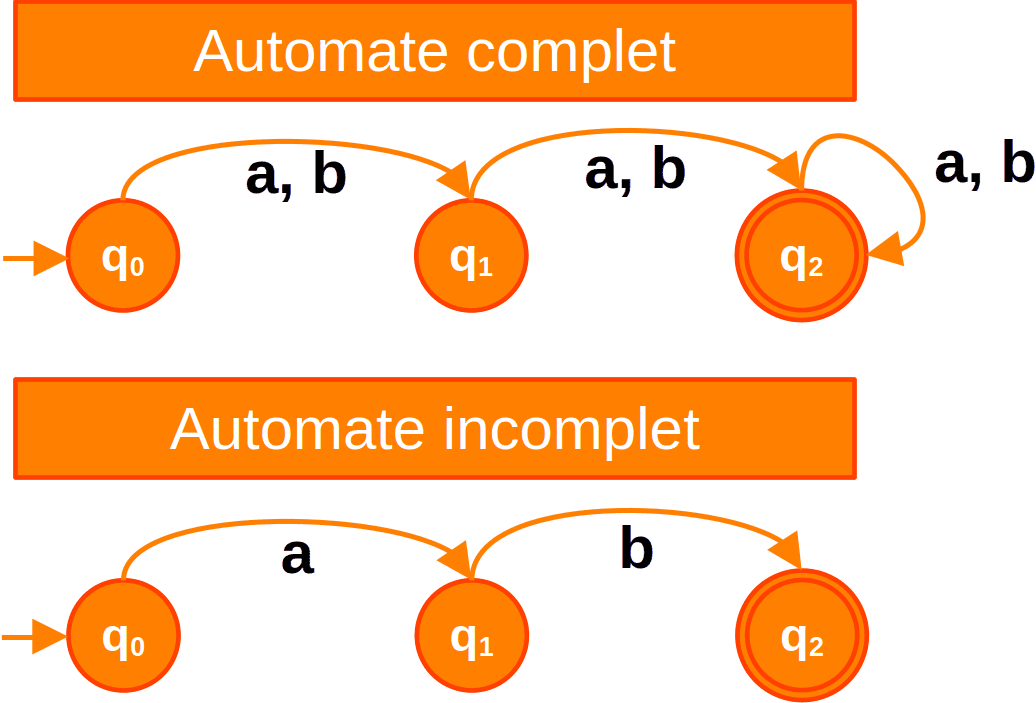
Automate complet et incomplet

Un automate fini peut être complet, avec pour chaque état et chaque symbole de l'alphabet, une transition qui est définie, ou incomplet, avec certains états pour lesquels aucune transition n'est spécifiée pour certains symboles de l'alphabet.

Un automate fini non-déterministe (AFN) $\mathcal{A}$ est défini par un quintuplet $(\Sigma, Q, \Delta, q_0, F)$, où :

• $\Sigma, Q, q_0, F$ sont définis comme dans un automate fini déterministe.
• $\Delta : Q \times (\Sigma \cup \{\epsilon\}) \to \mathcal{P}(Q)$ est une fonction de transition qui associe un ensemble d'états.

Il se différencie des automates déterministes par le fait qu'un même symbole peut se trouver sur plusieurs transitions partant d'un même état.

Exemple

Dans cet exemple, deux transitions issues de $q_0$ utilisent le symbole a, et deux transitions issues de $q_1$ utilisent le symbole b :

Transition spontanée

Une transition spontanée, ou $\epsilon$-transition (epsilon-transition), est une transition de la forme $\Delta(q, \epsilon) \ni q'$, où l'automate peut passer de l'état $q$ à $q'$ sans consommer de symbole d'entrée.

Exemple

Dans cet exemple, les $\epsilon$-transitions l'automate reconnaît les mots ab, b et c. Les $\epsilon$-transitions traversées sont neutres.

$\epsilon$-fermeture

Une $\epsilon$-fermeture d'un état ou d'un ensemble d'états est l'ensemble des états accessibles à partir de cet état (ou ensemble d'états) en utilisant uniquement des $\epsilon$-transitions.

Déterminisation et élimination

Déterminisation

Transformer un automate non-déterministe en automate déterministe consiste à réaliser les opérations suivantes :

• États : Chaque état de l'AFD correspond à un sous-ensemble $S \subseteq Q$ des états de l'AFN ;
• État initial : L'état initial est le singleton $\{q_0\}$ ;
• Transitions : Pour chaque $S \subseteq Q$ et $a \in \Sigma$, définir : $$\delta(S, a) = \epsilon\text{-fermeture}\left(\bigcup_{q \in S} \Delta(q, a)\right).$$
• États finaux : Tout état contenant un élément de $F$ est un état final.

Élimination des transitions spontanées

Éliminer les transitions spontanées consiste à réaliser les opérations suivantes :

• Calcul des $\epsilon$-fermetures : Pour chaque état $q \in Q$, déterminer tous les états accessibles par $\epsilon$-transitions.
• Révision des transitions : Remplacer toute transition $\Delta(q, a)$ par $\Delta'(q, a)$ tenant compte des $\epsilon$-fermetures.

Théorème de Kleene

Un langage est reconnu par un automate fini si et seulement s'il peut être décrit par une expression régulière.

Algorithme de Thompson

L'algorithme de Thompson propose une méthode pour produire un automate fini reconnaissant le même langage qu'une expression régulière donnée. Il propose de :

• Représenter chaque opérateur (concaténation, union, étoile) par des sous-automates ;
• Combiner récursivement les sous-automates.

Voici les sous-automates correspondants aux opérateurs :

Automate de Glushkov

Un automate de Glushkov est un automate sans $\epsilon$-transitions, lui aussi construit à partir d'une expression régulière dont il reconnaît le langage.

Langage local

Un langage $L$ défini sur un alphabet $A$ est dit local s'il existe trois ensembles $D \subseteq A$, $E \subseteq A$, et $F \subseteq A \times A$ tels qu'un mot $u$ appartient à $L$ si et seulement si :

• la première lettre de $u$ appartient à $D$,
• la dernière lettre de $u$ appartient à $E$,
• et aucun facteur de longueur 2 de $u$ n'appartient à $F$.

Algorithme de Berry-Sethi

L'algorithme de Berry-Sethi construit un automate de Glushkov sur un langage local en 4 étapes :

• Linéarisation de l'expression régulière r et r' ;
• Détermination des ensembles $D$, $E$ et $F$ ;
• Construction d'un automate sur le langage local obtenu ;
• Effacement des indices ajoutés lors de la linéarisation.

Stabilité des langages reconnaissables

Les langages reconnaissables sont stables par :

• Union finie : Si $L_1$ et $L_2$ sont reconnaissables, $L_1 \cup L_2$ l'est aussi ;
• Intersection finie : $L_1 \cap L_2$ est reconnaissable ;
• Complémentaire : $\Sigma^* \setminus L$ est reconnaissable.

Lemme de l'Étoile

Pour un langage $L$ reconnu par un automate à $n$ états :

Pour tout $u \in L$ avec $|u| \geq n$, il existe une décomposition $u = xyz$ telle que :

• $|xy| \leq n$,
• $y \neq \epsilon$,
• $xy^*z \subseteq L$.

Ce lemme formalise le comportement cyclique des automates pour des mots longs.