Arbre couvrant
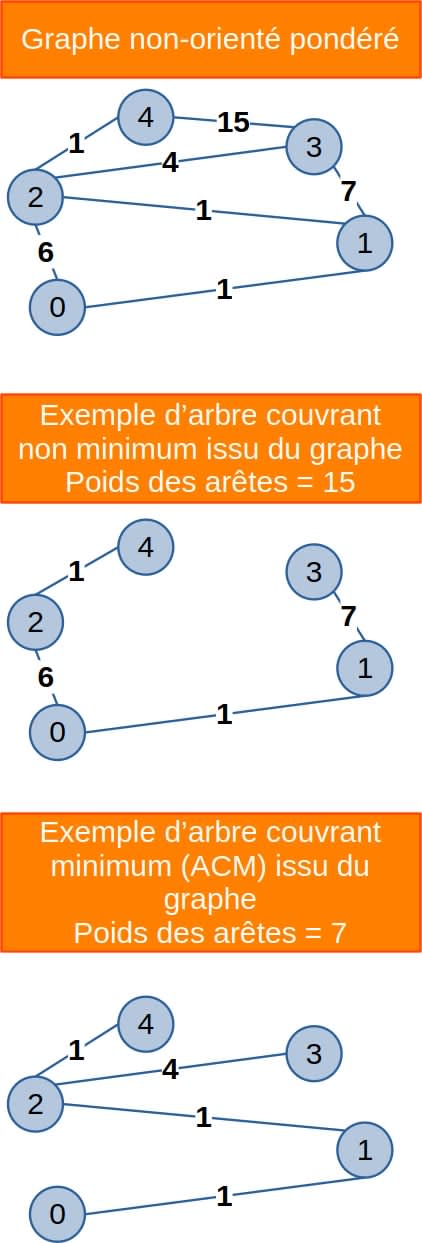
Un arbre couvrant d'un graphe non-orienté est un sous-ensemble de ses arêtes formant un arbre qui relie tous les sommets sans créer de cycle.
Dans le cas des graphes pondérés, un arbre couvrant de poids minimum (ACM) est un arbre couvrant dont la somme des poids des arêtes est minimale.
Algorithme de Kruskal
L'algorithme de Kruskal trouve un ACM à l'aide d'une approche gloutonne. Voici ses étapes principales :
- Tri des arêtes du graphe par poids croissant ;
- Initialisation d'un ensemble vide qui servira de sous-graphe vide pour stocker les arêtes de l'ACM ;
- Parcours des arêtes triées, et ajout des arêtes au sous-graphe si elles ne forment pas un cycle avec les arêtes déjà ajoutées.
L'algorithme se termine lorsque l'ACM est complet. L'arbre couvrant est formé quand toutes les arêtes nécessaires sont ajoutées (n-1 arêtes pour n sommets).
Pour détecter les cycles efficacement, on utilise une structure union-find. Cette structure permet de vérifier rapidement si deux sommets appartiennent à la même composante connexe.
Complexité
Cet algorithme est efficace, avec une complexité dominée par le tri des arêtes, soit $O(E\log E)$, où $E$ est le nombre d'arêtes. Les opérations d'union-find sont en $O(\alpha(V))$, quasi constantes « fonction d'Ackerman », pour $V$ sommets.


