Le vecteur vitesse
Construction d'un vecteur vitesse
Le vecteur vitesse moyen $\rm \overrightarrow{v}(t_2)$ au point $\rm M_2$ à la date $\rm t_2$ s'écrit :
$\boxed{\rm \overrightarrow{v}(t_2)=\dfrac{\overrightarrow{M_1 M_3}}{t_3-t_1}}$
Caractéristiques du vecteur vitesse
Le vecteur vitesse $\rm \overrightarrow{v}(t_2)$ possède quatre caractéristiques principales :
- Direction : la tangente à la trajectoire au point $\rm M _2$, parallèle à la droite $\rm (M _1 M _3)$
- Sens : celui du mouvement
- Valeur : $\rm v_2=\dfrac{M M_2}{t_3-t_1}=\dfrac{M_1 M_3}{2 \tau}$. La valeur $\rm v_2$ s'exprime en $\rm m.s^{-1}$.
($\tau$ : intervalle de temps constant entre deux points consécutifs) - Longueur : donnée par une échelle des vitesses
Échelle des vitesses : $\rm 1~cm \leftrightarrow 0,1~m.s^{-1}$
Le vecteur variation de vitesse
Construction du vecteur variation de vitesse
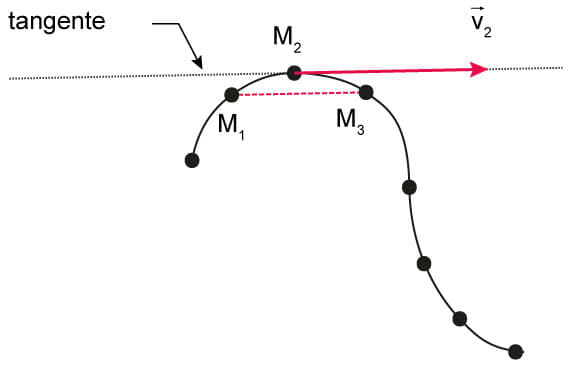
Pour construire le vecteur variation de vitesse $\bf \Delta \overrightarrow {V_5} = \overrightarrow {V_6} - \overrightarrow {V_4}$, il faut suivre ces étapes :
- Tracer les vecteurs vitesse $\rm \overrightarrow {V_4}$ et $\rm \overrightarrow {V_6}$
- Au point $\rm M_5$, reconstruire le vecteur $\rm \overrightarrow {V_6}$
- Construire le vecteur $-\rm \overrightarrow {V_4}$ depuis l'extrémité du vecteur $\rm \overrightarrow {V_6}$ reconstruit juste avant
- Le vecteur $\Delta \rm \overrightarrow {V_5}$ est le vecteur qui joint l'origine de $\rm \overrightarrow {V_6}$, point $\rm M_5$, à l'extrémité de $- \rm \overrightarrow {V_4}$
Principe fondamental de la dynamique
Le principe fondamental de la dynamique s'exprime par la relation suivante :
$\rm \displaystyle \sum \vec F_{ext} = m \times \Delta \overrightarrow v / \Delta t$

Le rôle de la masse du système
Plus la masse du système est grande, plus la variation du vecteur vitesse est faible pour une même somme des forces appliquées. Cette relation illustre l'inertie du système.