Fonctions affines

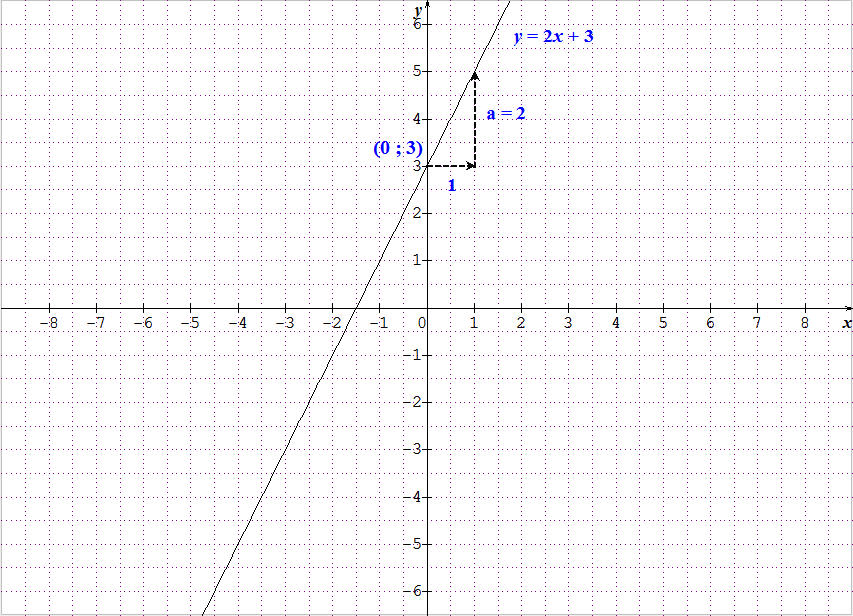
Fonction linéaire

Définition

La fonction linéaire de coefficient $a$ est la fonction :

$$x \mapsto a x$$

Représentation graphique

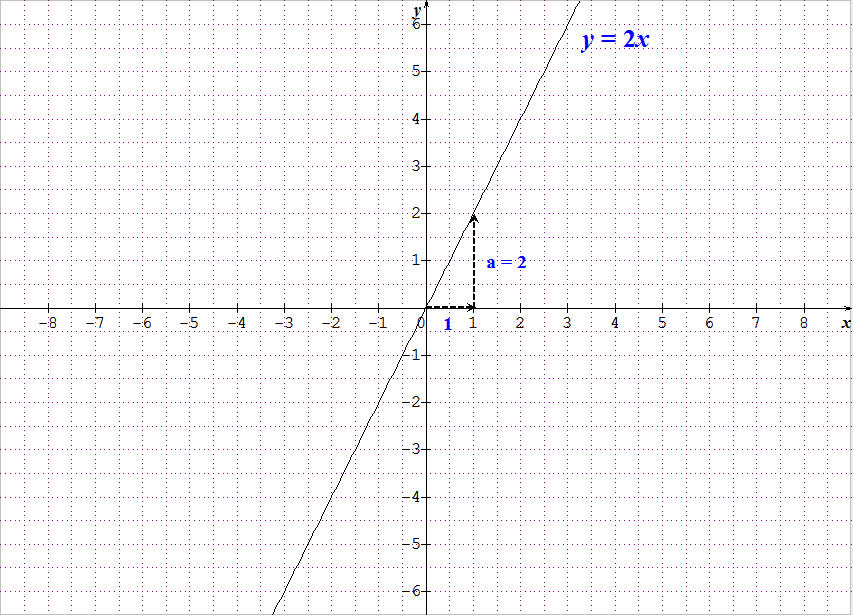
Sa représentation graphique est une droite qui passe par l'origine O du repère et par le point $(1~ ; a)$. Il suffit donc d'un deuxième point pour pouvoir la tracer. $a$ est le coefficient directeur de cette droite.

La droite ci-dessous représente graphiquement la fonction linéaire $x\mapsto 2x$ car elle passe par l'origine du repère et son coefficient directeur est $a = 2$.

Fonction affine

Une fonction affine est une fonction qui, pour tout nombre $x$, associe $ax + b$, où $a$ et $b$ sont deux nombres.

On note $f(x) = ax+b$ ou $f:x\mapsto ax+b$.

Représentation graphique

La représentation graphique d'une fonction affine est une droite qui passe par le point $(0~ ; b)$ car $f(0) = a \times 0 + b = b$. À partir du point $(0~ ; b)$, il suffit donc d'un deuxième point pour pouvoir tracer cette droite.

Paramètres de la fonction affine

$a$ est le coefficient directeur de la droite et $b$ son ordonnée à l'origine.

La droite ci-dessous représente graphiquement la fonction affine $x\mapsto 2x + 3$ car son ordonnée à l'origine est $b = 3$ et son coefficient directeur est $a = 2$.