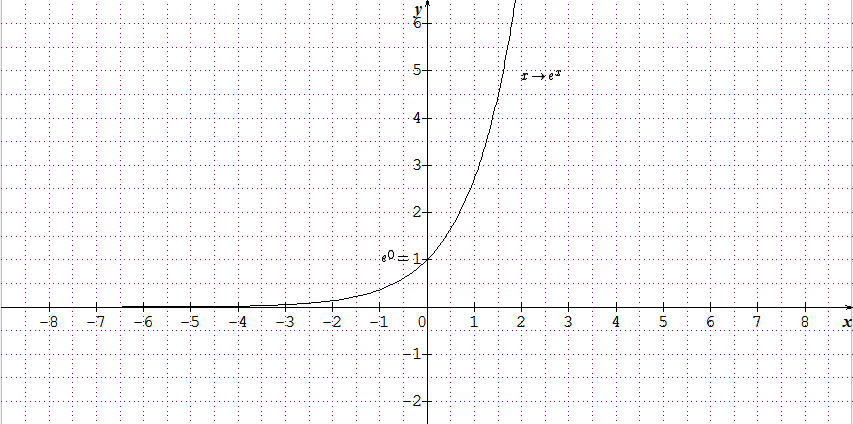
La fonction exponentielle
Définition
L'unique fonction $f$ définie et dérivable sur $\mathbb{R}$ vérifiant $f' = f$ et $f(0) = 1$ est la fonction exponentielle. Elle est notée $x \mapsto \exp(x) = {\mathrm{e}}^x$.
Propriétés algébriques
La fonction exponentielle possède plusieurs propriétés fondamentales qui facilitent les calculs :
- ${\mathrm{e}}^0 = 1$
- Pour tous nombres réels $x$ et $y$ :
| Propriété | Formule |
| Addition des exposants | ${\mathrm{e}}^{x + y} = {\mathrm{e}}^x \times {\mathrm{e}}^y$ |
| Exposant négatif | $\displaystyle {\mathrm{e}}^{-x} = \frac{1}{{\mathrm{e}}^x}$ |
| Soustraction des exposants | $\displaystyle {\mathrm{e}}^{x - y} = \frac{{\mathrm{e}}^x}{{\mathrm{e}}^y}$ |
| Puissance d'une exponentielle | ${({\mathrm{e}}^x)}^n = {\mathrm{e}}^{n x}$ ($n$ entier naturel) |