Algorithmes de recherche et de tri

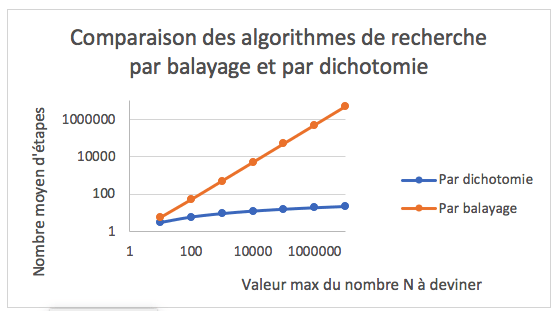
Recherche d'un nombre entier secret par balayage

Voici un programme Python qui permet d'effectuer la recherche d'un nombre entier secret avec la méthode par balayage.

Code du programme

$$\color{black}{\boxed{\scriptstyle{\textit{from random import *}\\ \textit{def ResultatEssai(essai,nombre_secret):}\\ \quad \textit{if essai < nombre_secret:}\\ \qquad\textit{return -1}\\ \quad\textit{elif essai == nombre_secret:}\\ \qquad\textit{return 0}\\ \quad\textit{return 1}\\ \quad\\ \textit{def recherche_pa_balayage(nombre_secret):}\\ \quad\textit{for i in range(1,101):}\\ \qquad\textit{if ResultatEssai(i,nombre_secret) ==0:}\\ \quad \qquad\textit{return i}\\ \quad \qquad\textit{nombre_secret = randint(1,101)}\\ \quad \qquad\textit{print(recherche_par_balayage(nombre_secret))}}}}$$

Fonctionnement de la fonction ResultatEssai

La fonction Python nommée ResultatEssai(essai,nombre_secret) retourne :

• -1 si le nombre essai est strictement inférieur au nombre secret
• 0 si le nombre essai est égal au nombre secret
• 1 si le nombre essai est strictement supérieur au nombre secret

Fonctionnement de la fonction de recherche

La fonction Python recherche_par_balayage(nombre_secret) effectue la recherche d'un nombre secret avec une méthode par balayage et retourne le nombre de tentatives.

Recherche par dichotomie en Python

Voici un programme Python qui permet d'effectuer la recherche d'un nombre entier secret avec la méthode par dichotomie.

Code du programme

Le programme se compose de deux fonctions principales qui travaillent ensemble pour trouver efficacement un nombre secret.

Fonctionnement du programme

La fonction ResultatEssai compare l'essai avec le nombre secret et retourne -1 si l'essai est trop petit, 0 s'il est correct, et 1 s'il est trop grand. La fonction recherche_par_dichotomie utilise cette comparaison pour ajuster les bornes de recherche et diviser l'intervalle par deux à chaque itération.

Le programme génère un nombre secret aléatoire entre 1 et 101, puis affiche le nombre de tentatives nécessaires pour le trouver avec l'algorithme de dichotomie.

Comparaison des algorithmes de recherche

Nombre maximum d'étapes

Le programme par balayage effectue au maximum 100 étapes (100 appels à la fonction ResultatEssai).

Le programme par dichotomie effectue au maximum 7 étapes (car $2^6 < 100$ et $2^7 > 100$).

Complexité générale pour un échantillon de taille N

Si la taille de l'échantillon à analyser est N, le nombre maximum d'étapes pour :

• L'algorithme de balayage est N ;
• L'algorithme de dichotomie est $E \left(\frac{\ln N}{\ln 2}\right)+1$ où $E()$ désigne la fonction partie entière et $\ln()$ la fonction logarithme népérien.

Nombre moyen d'étapes

On peut montrer que le nombre moyen d'étapes pour rechercher un entier compris entre 1 et N avec :

• La méthode par balayage est une fonction affine de N ;
• La méthode par dichotomie est une fonction affine du logarithme népérien de N.

Visualisation comparative

On visualise avec ce graphique le fait que l'algorithme de recherche par dichotomie est en moyenne beaucoup plus efficace que celui par balayage.

Algorithmes de tri

Un algorithme de tri permet de trier des données numériques ou alphabétiques. Nous traiterons ici des données numériques stockées dans un tableau à une dimension.

Implémentation d'un tri par ordre décroissant

Voici un programme Python qui implémente une fonction nommée tri_liste_non_en_place(liste) qui permet de trier par ordre décroissant la liste de nombres nommée "liste" à l'aide de deux autres listes "nliste" et "bliste".

$$\boxed{\scriptstyle{\textit{from random import *}\\ \text{def tri_liste_non_en_place(liste):}\\ \quad\text{nliste = [0 for i in range(len(liste))]}\\ \quad\text{bliste = [False for i in range(len(liste))]}\\ \quad\text{for i in range(len(liste)):}\\ \qquad\text{max = -1}\\ \qquad\text{for j in range(len(liste)):}\\ \qquad \quad\text{if not(bliste[j]) and (max == -1 or liste[j] > max):}\\ \qquad \qquad\text{max = liste[j]}\\ \qquad \qquad\text{ind_max = j}\\ \qquad\text{nliste[i] = max}\\ \qquad\text{bliste[ind_max] = True}\\ \quad\text{return nliste}\\ \quad \\ \text{liste = [randint(1,1000) for i in range(10)]}\\ \text{print("Liste non triée",liste)}\\ \text{print("Liste triée",tri_liste_non_en_place(liste))}}}$$

Principe de fonctionnement

Cet algorithme utilise deux listes auxiliaires pour effectuer le tri sans modifier la liste originale. La liste nliste stocke les éléments triés, tandis que la liste bliste marque les éléments déjà traités.

$$\boxed{\scriptstyle{\text{Liste non triée [728, 144, 564, 819, 130, 886, 801, 130, 900, 568]}\\ \text{Liste triée [900, 886, 819, 801, 728, 568, 564, 144, 130, 130]}}}$$

Les algorithmes de tri en place

Il est possible de trier les données à partir d'un seul tableau. On dit alors qu'on effectue un tri sur place. Il existe plusieurs algorithmes de tri en place qui ont des efficacités différentes. Nous allons en étudier plusieurs.

a) Tri par insertion

Le tri par insertion est un algorithme de tri classique dont le principe est très simple. C'est le tri que la plupart des personnes utilisent naturellement pour trier des cartes : prendre les cartes mélangées une à une sur la table, et former une main en insérant chaque carte à sa place.

Voici un algorithme de tri par insertion en pseudo-code :

$\color{blue}{\text{procédure tri_insertion (tableau T, entier n)}\\ \qquad \text{pour i de 1 à n-1}\\ \qquad \quad \rm x \leftarrow T[i]\\ \qquad \quad \rm j \leftarrow i\\ \qquad \quad \text{tant que j > 0 et T[j - 1] > x}\\ \qquad \qquad \rm T[j] \leftarrow T[j - 1]\\ \qquad \qquad \rm j \leftarrow j - 1\\ \qquad \quad\text{fin tant que}\\ \qquad \quad \rm T[j]\leftarrow x\\ \qquad \text{fin pour}\\ \quad\text{fin procédure}}$

Les éléments du tableau T sont numérotés de 0 à n – 1.

b) Complexité du tri par insertion

On montre (avec des maths !!) qu'en moyenne le nombre de boucles effectuées pour un tableau de taille n est $\displaystyle {\rm \frac{n^2}{4}}$

c) Des algorithmes de tri plus efficaces

Il existe d'autres algorithmes de tri :

• Tri à bulles (bubble sort)
• Tri par sélection (selection sort)
• Tri fusion (merge sort)
• Tri rapide (quick sort)

d) Complexité des algorithmes de tri

On trouve la complexité des algorithmes de tri dans le tableau suivant :

Les algorithmes les plus efficaces en moyenne sont ceux de tri par fusion ou de tri rapide.

Tri par sélection

Avec le tri par insertion, le tri par sélection est la seconde méthode de tri à connaître en première NSI.

Algorithme de tri par sélection

Voici un algorithme de tri par insertion en pseudo-code :

$\color{blue}{\text{procédure tri_selection(tableau T)}\\ \qquad \text{n ← longueur(T)}\\ \qquad \text{pour i de 0 à n - 2}\\ \qquad \quad \rm min ← i\\ \qquad \quad \text{pour j de i + 1 à n - 1}\\ \qquad \qquad \rm si T[j] < T[min], alors \space min ← j\\ \qquad \quad\text{fin pour}\\ \qquad \quad \rm si \space min ≠ i, alors \space échanger \space T[i] \space et \space T[min]\\ \qquad \text{fin pour}\\ \quad\text{fin procédure}}$

Les éléments du tableau T sont numérotés de 0 à n – 1.

Efficacité et complexité

Le tri par insertion et le tri par sélection sont équivalents en terme d'efficacité et de complexité algorithmique. Ainsi, on peut montrer qu'en moyenne le nombre de tours de boucles effectués pour un tableau de taille n est $\displaystyle {\rm \frac{n^2}{4}}$.

Classes de complexité

Dans la fiche précédente, la notion de complexité a été abordée. Au niveau du vocabulaire technique, on va souvent indiquer ce qu'on appelle la classe de complexité d'un algorithme :

• La classe de complexité d'un algorithme dont la complexité est de 1 sera dite constante ;
• La classe de complexité d'un algorithme dont la complexité est de N sera dite linéaire ;
• La classe de complexité d'un algorithme dont la complexité est de N² sera dite quadratique ;
• La classe de complexité d'un algorithme dont la complexité est de log(N) sera dite logarithmique ;
• La classe de complexité d'un algorithme dont la complexité est de N.log(N) sera dite quasi-linéaire.

Classification des algorithmes étudiés

Ainsi la recherche par balayage fait partie de la classe de complexité linéaire, alors que la recherche dichotomique fait partie de la classe de complexité logarithmique. Les algorithmes de tri par insertion et par sélection sont tous deux dans la classe de complexité quadratique.