Intensité du courant électrique
L'intensité du courant à un endroit du circuit mesure le débit de charge électrique à cet endroit. L'intensité du courant qui arrive sur une armature du condensateur est la dérivée par rapport au temps de la charge électrique portée par cette armature :
$$i = \dfrac{\mathrm dq}{\mathrm dt}\left|\begin{array}{lll}i = \text{ intensité en ampère A}\\t = \text{ le temps en seconde s}\\q = \text{ la charge en en coulomb C}\end{array}\right.$$
Condensateur
Un condensateur est composé de deux armatures chargées électriquement et d'un isolant.
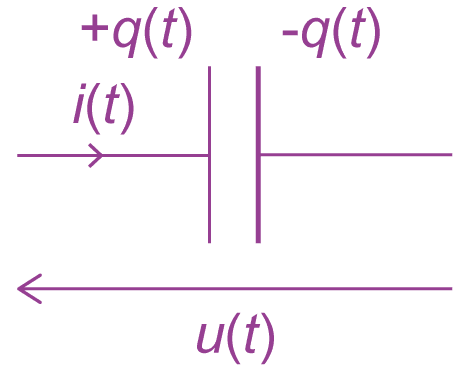
La charge $q$ stockée par le condensateur est :
$$\boxed{q(t) = \mathrm C~u_{\rm C}(t) \Rightarrow i_{\rm C} (t) = \frac{\mathrm dq(t)}{\mathrm dt} = \mathrm C \frac{du_{\mathrm C}(t)}{\mathrm dt}}$$
Avec $\rm C =$ capacité du condensateur en Farad $\rm (F)$.
Charge du condensateur
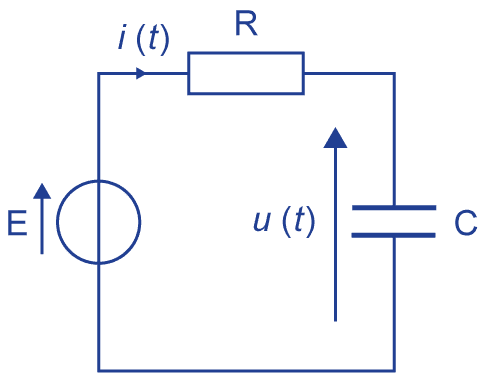
D'après la loi des mailles :
$$\mathrm E = u(t) + \mathrm R~ i(t)$$
$$\mathrm E = u(t) + \mathrm R~ \mathrm C\dfrac{\mathrm du(t)}{\mathrm dt}$$
Posons $\rm \tau = RC$ avec $\tau$ constante de temps d'un condensateur en seconde.
Solution
$$u(t) = u_h + u_p \Rightarrow u(t) = \mathrm{A~e}^{-\dfrac{t}{\tau}} + \mathrm E$$
Condition limite à $\rm t = 0$, $\rm u(t) = 0 \Rightarrow A = -E$
$$\boxed{u(t) = \mathrm E \left(1 - \mathrm e^{-\dfrac{t}{\tau}}\right)}$$
Détermination de $\tau$

- Pour $t = \tau$, $u(t) = 0,63~\mathrm E$
- La tangente en $t = 0$ à la courbe coupe l'asymptote $u = \mathrm E$ en $t = \tau$.


