Définition
On considère une fonction $f$ continue sur l'intervalle $[a ; b]$ ($a < b$) et on note $\mathrm F$ une de ses primitives. Cette définition établit le lien fondamental entre les primitives et les intégrales définies.
On a :
$$\int_{a}^{b} f(x) dx = [\mathrm F(x)]_{a}^{b} = \mathrm F(b) - \mathrm F(a)$$
Exemple
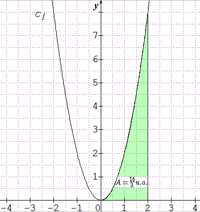
La fonction $f$ définie par $f(x) = 2{x}^2$ est continue sur l'intervalle $[0 ; 2]$ et une de ses primitives sur cet intervalle est la fonction $F$ définie par $\mathrm F(x) = \frac{2{x}^3}{3}$.
$$\int_0^2 f(x) \mathrm dx = \left[\frac{2{x}^3}{3}\right]_0^2 = \frac{16}{3}$$
Propriétés
Pour $f$ et $g$ deux fonctions continues sur l'intervalle $[a ; b]$ ($a < c < b$) et un réel $k$, nous avons les propriétés suivantes :
Linéarité de l'intégrale
Additivité :
$$\int_{a}^{b} (f(x) + g(x)) \mathrm dx = \int_{a}^{b} f(x) \mathrm dx + \int_{a}^{b} g(x) \mathrm dx$$
Homogénéité :
$$\int_{a}^{b} k f(x) \mathrm dx = k \int_{a}^{b} f(x) \mathrm dx$$
Relation de Chasles
$$\int_{a}^{b} f(x) \mathrm dx = \int_{a}^{c} f(x) \mathrm dx + \int_{c}^{b} f(x) \mathrm dx$$
Propriétés de comparaison
Positivité : $f(x) > 0$ sur $[a ; b] \Rightarrow \int_{a}^{b} f(x) \mathrm dx > 0$
Croissance : $f(x) > g(x)$ sur $[a ; b] \Rightarrow \int_{a}^{b} f(x) \mathrm dx > \int_{a}^{b} g(x) \mathrm dx$
Intégration par parties
Soit $f$ et $g$ deux fonctions continues et dérivables sur $[a ; b]$ ($a < b$). On suppose que les fonctions dérivées de $f$ et $g$ sont continues sur $[a ; b]$.
On a la formule d'intégration par parties :
$$\int_a^b f(x) g'(x) \mathrm{d}x = [f(x)\times g(x)]_a^b - \int_a^b g(x) f'(x) \mathrm{d}x$$