Les réglages des asservissements (PID)

Rappels sur les systèmes asservis

L'asservissement est utilisé dans les systèmes automatisés pour assurer le suivi précis d'une consigne. Il repose sur une boucle de rétroaction qui ajuste continuellement la sortie en fonction de l'écart entre la consigne et la mesure réelle.

Dans une commande en boucle ouverte, il n'y a pas de retour d'information sur la sortie. Ce type de commande est simple, mais sensible aux perturbations et aux variations des conditions de fonctionnement.

Une commande en boucle fermée utilise un capteur pour comparer la sortie réelle à la consigne et ajuster en conséquence la commande du système. Ce type d'asservissement permet de corriger les écarts et de stabiliser le système.

Performances des systèmes asservis

Les performances d'un système asservi sont évaluées à travers plusieurs critères essentiels :

• Précision : capacité du système à réduire l'écart entre la consigne et la sortie en régime permanent. Une faible erreur statique est indicative d'une haute précision.
• Rapidité : temps que met le système pour atteindre la consigne après une perturbation ou une modification de celle-ci. Une réponse rapide est souvent souhaitée pour améliorer l'efficacité opérationnelle.
• Amortissement : aptitude du système à atténuer les oscillations autour de la consigne. Un bon amortissement prévient les dépassements excessifs et assure une convergence stable vers la valeur souhaitée.
• Stabilité : capacité du système à revenir à un état d'équilibre après une perturbation. Un système stable ne présente pas de comportements divergents ou oscillatoires indésirables.
• Robustesse : capacité du système à maintenir ses performances malgré les variations des conditions externes ou des paramètres internes. Un système robuste fonctionne de manière fiable même en présence d'incertitudes ou de perturbations.

Correcteurs PID

Le régulateur est un outil fondamental en automatisation pour contrôler les systèmes dynamiques. Il combine trois actions distinctes :

• Proportionnelle (P) : cette composante génère une action de contrôle proportionnelle à l'erreur actuelle (la différence entre la consigne et la mesure). Un gain proportionnel élevé augmente la réactivité du système, mais peut induire des oscillations et potentiellement déstabiliser le système.
• Intégrale (I) : elle s'intéresse à l'accumulation des erreurs passées. En intégrant l'erreur sur le temps, cette composante vise à éliminer l'erreur statique, améliorant ainsi la précision en régime permanent. Toutefois, une action intégrale trop forte peut ralentir la réponse du système et provoquer des oscillations.
• Dérivée (D) : cette composante anticipe les variations futures de l'erreur en se basant sur sa dérivée. Elle apporte une correction en fonction de la vitesse de changement de l'erreur, améliorant ainsi la stabilité et réduisant le dépassement. Cependant, une action dérivée excessive peut rendre le système trop sensible au bruit.

L'ajustement optimal des gains proportionnel (Kp), intégral (Ki) et dérivé (Kd) est crucial pour obtenir un comportement souhaité du système. Des méthodes empiriques, comme la méthode de Ziegler-Nichols, sont souvent utilisées pour déterminer ces paramètres de manière efficace.

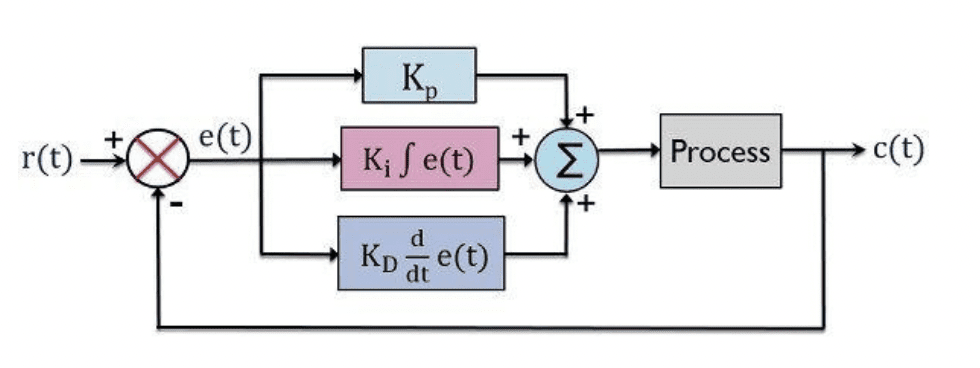
Le PID (Proportionnel-Intégral-Dérivé) combine les avantages des trois correcteurs pour un contrôle optimal. Il ajuste en permanence la commande pour garantir un équilibre entre rapidité, précision et stabilité.