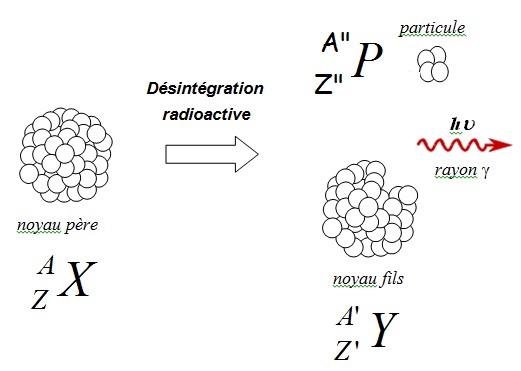
Réactions nucléaires

Réactions nucléaires spontanées

Lors d'une désintégration radioactive, un nucléide $^A_ZX$ (noyau père) donne spontanément une particule $^{A’’}_{Z’’}P$ , un rayonnement $\gamma$ (gamma) électromagnétique et un autre nucléide $^{A’}_{Z’}Y$ (noyau fils).

Il existe 3 types de particules $^{A’’}_{Z’’}P$ : 

• Particule $\alpha$ notée $^4_2He$ ;
• Particule $\beta^-$ notée : $^0_{-1}e$ (électron) ;
• Particule $\beta^+$ notée $^0_1e$ (positon).

Lors d'une désintégration radioactive, le nombre de masse $A$ et le nombre de charge $Z$ sont conservés. L’activité notée $A$ d’une substance radioactive est le nombre de désintégrations que l’on observe en une seconde. Elle se compte en becquerel (Bq) : $1 \:Bq = 1$ désintégration/seconde.

Réactions nucléaires provoquées

La fission est une réaction nucléaire provoquée au cours de laquelle un noyau lourd, percuté par un neutron de faible énergie, se scinde généralement en deux noyaux plus légers avec production de 2 ou 3 neutrons.
La fusion nucléaire est obtenue en obligeant deux noyaux (nucléides) légers à fusionner pour former un nucléide plus lourd. Ce processus s’accompagne d’un fort dégagement d’énergie à l’origine de la lumière produite par les étoiles. 

Energie dégagée par les réactions nucléaires

Lors d'une réaction nucléaire, de la masse est convertie en énergie selon l'équivalence donnée par la relation : $E = \Delta m \times c^2$
E en Joule (J) ; $\Delta m$ (variation de masse entre les réactifs et les produits de la réaction nucléaire) en kg ; $c = 3,00 \times 10^8\: m.s^{-1}$ (célérité de la lumière dans le vide).

Un noyau radioactif est un noyau instable dont la désintégration est aléatoire et s’accompagne de :

• L’apparition d’un nouveau noyau
• L’émission d’une particule notée $\alpha , \beta ^{+},\beta ^{-}$
• L’émission d’un rayonnement électromagnétique noté $\gamma$

Loi de conservation (loi de Soddy)

Lors d’une désintégration radioactive $\alpha$ ou $\beta$, il y a conservation de la charge électrique du noyau $\mathrm Z$ (conservation du nombre de protons et du nombre) de nucléons $\mathrm A$.

Désintégration alpha ($\alpha$)

Des noyaux sont dits radioactifs $\alpha$ s'ils expulsent des noyaux d’hélium $\mathrm{ _{2}^{4} He}$ .
D’après la loi de Soddy, l’équation s’écrit :

$\mathrm{ _{Z}^{A} X \rightarrow _{Z-2}^{A-4} Y + _{2}^{4} He }$

Désintégration $\mathrm{ \beta ^{-} }$(émission d’un électron)

Des noyaux sont dits radioactifs $\mathrm{ \beta ^{-} }$ s’ils émettent des électrons notés ${ _{-1}^{0} e }$.
D’après la loi de Soddy l’équation s’écrit :

$\mathrm{ _{Z}^{A} X \rightarrow _{Z+1}^{A} Y + _{-1}^{0} e }$

Désintégration $\mathrm{ \beta ^{+}}$(émission d’un positron)

Des noyaux sont dits radioactifs $\mathrm{ \beta ^{-} }$ s’ils émettent des électrons notés $\mathrm{ _{+1}^{0} e }$.
D’après la loi de Soddy l’équation s’écrit :

$\mathrm{ _{Z}^{A} X \rightarrow _{Z-1}^{A} Y + _{+1}^{0} e }$

La désexcitation $\mathrm{\gamma }$

Après une transformation radioactive du noyau, le noyau fils est dans un état excité ($^*$) et se désexcite en émettant un (ou plusieurs) photons de haute énergie (gamma).

$\mathrm{ _{Z}^{A} Y^* \rightarrow _{Z}^{A} Y + \gamma}$

Loi de décroissance radioactive

$\mathrm{N(t)= N_0 * e^{- \lambda t}}$

Avec :

• N(t) : le nombre de noyau présent à l’instant t
  $\lambda$ : est la constante radioactive, elle est caractéristique d’un radioélément.
• T : le temps 

Constante de temps

L'inverse de la constante radioactive est homogène à une durée (à la même dimension qu'une durée ou s'exprime avec la même unité qu'une durée). On écrira : 

$\mathrm{ \tau= \frac{1}{\lambda }}$

Temps de demi-vie radioactive

La demi-vie radioactive, notée $t_{\frac{1}{2}}$, d'un échantillon de noyaux radioactifs est égale à la durée nécessaire pour que, statistiquement, la moitié des noyaux radioactifs présents dans L’échantillon se désintègrent.

$t_{\frac{1}{2}} = \frac{\ln 2}{\lambda}$

Activité d’une source radioactive

L'activité A d'une source radioactive est égale au nombre moyen de désintégrations par seconde dans l'échantillon. Elle s'exprime en becquerels dont le symbole est Bq (1Bq = 1 désintégration par seconde).

$A(t)= \lambda * N(t)$

Où :

$A(t)= A_0 e^{- \lambda t}$

Avec :

$A_0 = \lambda * N_0$