Une charge $q$ qui se déplace avec une vitesse $\vec v$ dans un champ magnétique caractérisé par le vecteur $\vec B$ subit une force magnétique appelée force de Lorentz $\vec f_m$ donnée par :
$\vec f_m = q\vec v \land \vec B$
$\vec f_m$ est le produit vectoriel de $q \vec v$ par $\vec B$.
direction : perpendiculaire au plan formé par $q \vec v$ et $\vec B$.
sens : déterminé par la règle des trois doigts de la main droite (cf. figure).
norme : $f_m = \vert qvB \sin \alpha \vert$
avec : $q$ est la charge (C)
$v$ est la vitesse de la charge (m/s)
$B$ est l'intensité (la norme) du vecteur champ magnétique (T)
$\alpha$ est l'angle formé par $q \vec v$ et $\vec B$.
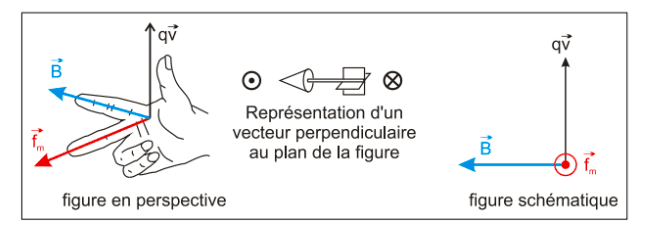
Force de Lorentz : $\vec f_m = q\vec v \land \vec B$
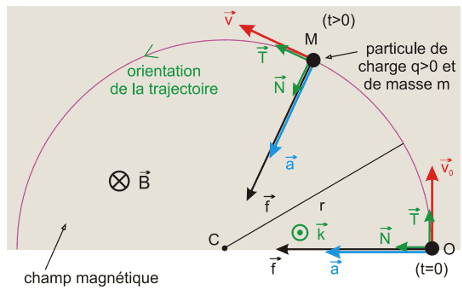
Le poids $\vec P$ est négligeable devant $\vec f_m$. Il n'y a pas de frottement car le mouvement se fait dans le vide.
La relation fondamentale de la dynamique s'écrit :
$q\vec v \land \vec B = m \vec a$
$\vec a = \frac{q}{m}\vec v \land \vec B$
Projections sur les directions de $\vec k$, $\vec T$, $\vec N$ :
$a_k = 0$ (1) car
$a_r$ (2) car
$\displaystyle a_N = \frac{\vert q\vert v B}{m}$ (3) car
(1) : $\displaystyle a_k = \frac{d v_k}{d t} = 0$ $\Rightarrow v_k = \text{constant} = v_{0k} = 0$
Donc il n'y a pas de mouvement suivant $k$ !
-> Le mouvement est plan. Il s'effectue dans un plan perpendiculaire à $\vec B$, contenant la vitesse initiale $\vec v_0$
(2) : $\displaystyle a_T = \frac{d v_T}{d t} = 0 \Rightarrow v_ T = v = \text{constant}$ !
-> Le mouvement est uniforme.
Comme la coordonnée normale de l'accélération s'écrit toujours $\displaystyle a_N = \frac{v^2}{\rho}$ ($\rho =$ rayon de courbure du cercle tangent), on a grâce à (3) :
$\displaystyle \frac{\vert q\vert v B}{m} \Leftrightarrow \rho = \frac{m v }{\vert q\vert B}$ $m, \:v, \: q\: et\: B$ sont constants $\Rightarrow \rho = R$ est constant !
-> Le mouvement est circulaire.
Une particule chargée entrant dans un champ magnétique avec une vitesse perpendiculaire à $\vec B$ décrit un MCU dans un plan perpendiculaire au champ.
Le rayon de la trajectoire est donné par l'expression : $\displaystyle R = \frac{m v}{\vert q\vert B}$ (4)


