Effet photoélectrique / Niveaux d’énergie de l’atome

Un faisceau de lumière blanche est dispersé par un prisme. Le faisceau émergent est constitué de toutes les couleurs de l’arc-en-ciel. Ce phénomène est la dispersion de la lumière. La figure colorée observée sur un écran est le spectre de la lumière blanche.

La lumière blanche est constituée de plusieurs lumières (ou radiations) colorées. C’est une lumière polychromatique. Le laser est constitué d'une seule radiation : c’est une lumière monochromatique.
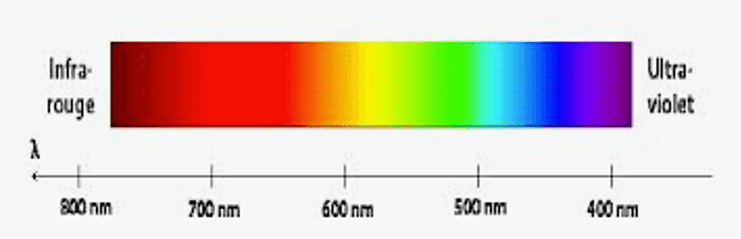
Un rayonnement monochromatique  est caractérisé, dans le vide, par une grandeur appelée longueur d’onde, notée $\lambda$. Elle s’exprime en mètre ou plus souvent en nanomètre (nm). On note $\rm 1\: nm = 10^{-9}\: m$. 
L’œil n’est sensible qu’aux rayonnements compris entre 400 et 750 nm.

Les spectres d’émission

• Les spectres d’émission d’origine thermique : Un corps fortement chauffé produit un rayonnement d’origine thermique dont le spectre est continu.
  Quand la température augmente, le spectre s’enrichit en radiations de courtes longueurs d’onde.

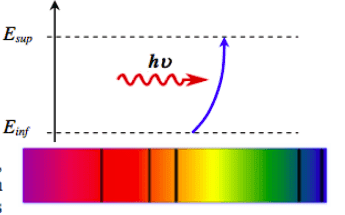
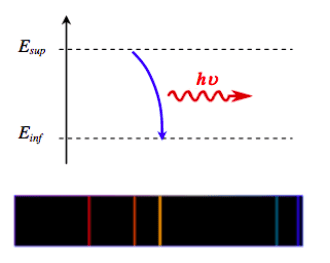
• Les spectres de raies : Un gaz d’atomes excités à basse pression émet une lumière composée d’une ou plusieurs radiations sur un fond noir. Son spectre est constitué de raies colorées. Le spectre de raies d’émission est caractéristique de l’atome ou de l’ion qui émet la lumière.

Une onde électromagnétique est caractérisée par sa fréquence $v$(en $\rm Hz$) ou par sa longueur d’onde $\lambda$ (en $\rm m$). Elle transporte de l’énergie mais pas de matière. Elle peut se propager dans le vide. La lumière peut être décrite par une onde électromagnétique d’où le modèle ondulatoire. 

$\color{purple}{\begin{array}{|c|}
\hline
\color{black}{\displaystyle \lambda = \frac{c}{v}}\\
\hline
\end{array}}$ avec $\lambda$ en $\rm m$, $c$ vitesse de propagation de la lumière dans le vide en $\rm m.s^{-1}$ et $ν$ en $\rm Hz$.

\[c = 3,00 \cdot 10^8~\rm m.s^{-1}\]

Le domaine de la lumière visible s’étend de $400$ à $\rm 800~nm$.

Une onde électromagnétique de fréquence $\nu$ ou de longueur d’onde $\lambda$ peut aussi être décrite par des photons qui transportent chacun un quantum d’énergie $\rm E$ : 

$\displaystyle E = h \times \nu = \frac{h \times c}{\lambda}$

avec $\rm E$ en Joule $\rm (J)$, $h$ constante de Planck (en $\rm J.s$).

Les niveaux d’énergie d’un atome sont quantifiés et ne prennent que certaines valeurs. 

L’état de plus haute énergie correspond à l’état ionisé $\rm E_{\infty} = 0 \:\rm eV$. Les énergies des autres niveaux sont négatives.

Absorption de la lumière par un atome

Un atome qui se retrouve dans unétat caractérisé par un niveau d'énergie $E_{inf}$ peut absorber certains photons d'énergie $E$ bien précise et passer dans un état d'énergie $E_{sup}$ supérieure.

L'énergie $E$ de ce photon correspond à l'énergie gagnée par l'atome :

$E = E_{sup} - E_{inf}$
 
Ainsi, la longueur d'onde du photon absorbé est :

$\displaystyle E = \frac{hc}{\lambda}$ $\Leftrightarrow$ $\displaystyle \lambda = \frac{hc}{E} = \frac{hc}{E_{sup} - E_{inf}}$

Comme tous les atomes possèdent des niveaux d'énergie bien définis, ils ne peuvent absorber que certains photons de longueur d'onde bien précise. Ceci conduit, dans le domaine du visible, à l'observation des raies noires dans le spectre de raies d'absorption.

Emission de la lumière par un atome :

Un atome qui se retrouve dans un état excité (par décharhe électrique, absorption de lumière, chauffage, etc.) caractérisé par un niveau d'énergie $E_{sup}$ retourne spontanément dans son état fondamental ou dans un état excité de moindre énergie $E_{inf}$ en émettant un photon.

$E = E_{sup} - E_{inf}$

Ainsi, la longueur d'onde du photon émis sera :

$\displaystyle E = \frac{hc}{\lambda}$ $\Leftrightarrow$ $\displaystyle \lambda = \frac{hc}{E} = \frac{hc}{E_{sup} - E_{inf}}$

Comme tous les atomes possèdent des niveaux d'énergie bien définis, ils ne peuvent émettre que certains photons de longueur d'onde bien précise correspondant à une transition énergétique possible de l'atome. Ceci conduit, dans le domaine du visible, à l'observation des raies de couleurs dans le spectre de raies d'émission.