L’intensité du courant à un endroit du circuit mesure le débit de charge électrique à cet endroit. Ainsi, l’intensité du courant qui arrive sur une armature du condensateur est la dérivée par rapport au temps de la charge électrique portée par cette armature :
$i = \dfrac{dq}{dt}$
Avec :
- $i$ : intensité en $A$
- $t$ : le temps en seconde
- $q$ : la charge en en coulomb
La capacité d’un condensateur est définie par la relation suivante :
$q = C \times U_c$
Avec :
- $q$ : la charge stockée sur la borne positive du condensateur en coulomb $(C)$.
- $Uc$ : la tension électrique aux bornes du condensateur en volt $(V)$
- $C$ : la capacité du condensateur en Farad $(F)$
Le dipôle $(RC)$
On considère le circuit RC ci-dessous tel qu’à $t=0$ le condensateur est déchargé.
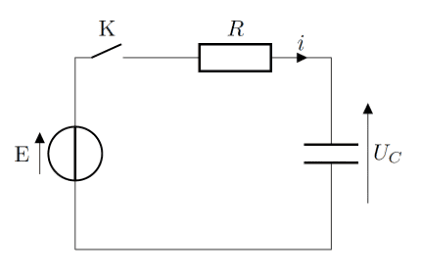
À $t=0$, on ferme l’interrupteur K.
La loi des mailles donne :
$U_c + U_r = E$
La loi d’Ohm $U_r = R \times i$
$U_c + U_r = E \Rightarrow R \times i + \dfrac{q}{C} = E$
$R \times \dfrac {dq(t)}{dt} + \dfrac{q}{C} = E$
$\dfrac{dq(t)}{dt} + \dfrac{q}{R \times C} = \dfrac{E}{R}$



