Travail de la force électrique :
Bilan énergétique : $\rm e = 1,602\cdot^{-19}C$, $\rm m = 9,109\cdot 10^{-31}~kg$.
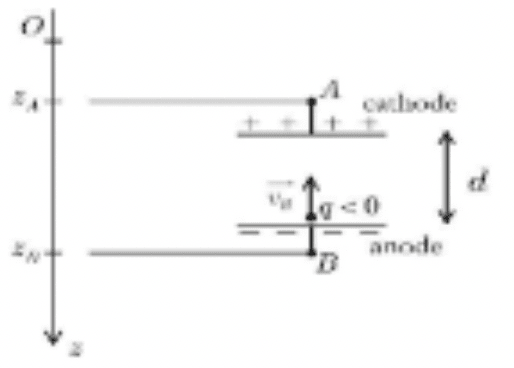
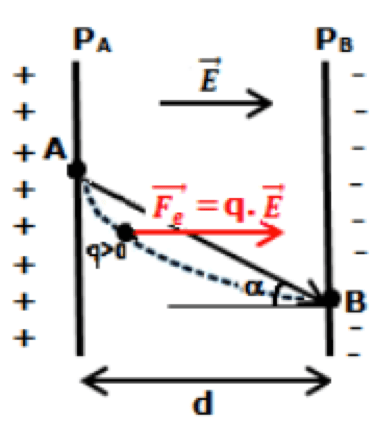
On considère une charge $q < 0$ allant de l'anode $\rm (B)$ à la cathode $\rm (A)$ avec un mouvement rectiligne sous l'effet d'un champ constant $\overrightarrow{\rm E}}$. On cherche la vitesse en $\mathrm A = \overrightarrow{v_{\rm A}}$.
Le travail élémentaire de ce champ est donné par :
$\delta \mathrm W = \overrightarrow{\rm F}d\overrightarrow{\rm OM} = +Q\mathrm Edz$ $\Rightarrow$ $\displaystyle \rm W_{BA} = \int^{\mathcal z_A}_{\mathcal z_B}\mathcal qE\mathcal{dz}$ $= q\mathrm E(z_{\rm A} - z_{\rm B})= -q\mathrm E d$ car $z_{\rm A} - z_{\rm B} = -d < 0$.
Or $\displaystyle \rm E = \frac{U}{\mathcal d}$ donc $\rm W_{AB} = - \mathcal qU = \mathcal q(V_B - V_A)$. Ce travail est moteur si $q<0$.
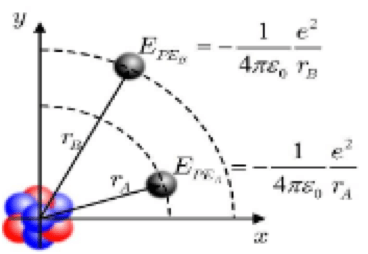
Energie potentielle électrique $\color{green}{\bf E_{PE}}$ $\boxed{\mathrm{E_{PE}} = + \frac{1}{4\pi\varepsilon_0}\frac{qq'}{f}}$
Travail de la force électrostatique :
D'un rayon $r_{\rm A}$ à un rayon $r_{\rm B}$, $\displaystyle \mathrm{W_{AB}}(\overrightarrow{\rm F_{NIE}}) = \int^{\mathcal r_B}_{\mathcal r_A} + \frac{1}{4\pi\varepsilon_0}\frac{qq'}{r^2}dr$ $= \displaystyle \left[-\frac{1}{4\pi\varepsilon_0}\frac{qq'}{r}\right]^{r_{\rm B}}_{r_{\rm A}}$ $\displaystyle = + \frac{qq'}{4\pi\varepsilon_0}\left(\frac{1}{r_{\rm A}} - \frac{1}{r_{\rm B}}\right)$.