Polynômes, cosinus et sinus

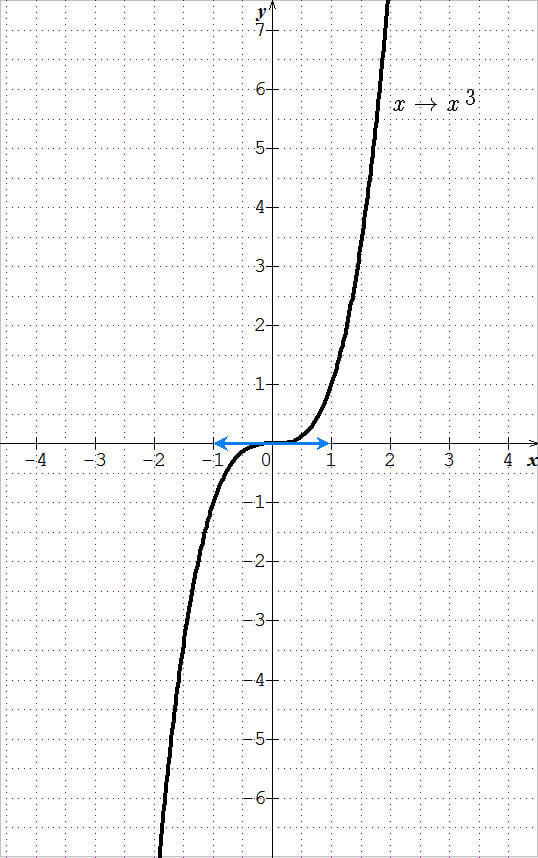
La fonction cube est la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = x^3$.

Pour tout $x\in \mathbb{R}$, $f(-x) = -f(x)$ donc $f$ est impaire et sa courbe représentative est symétrique par rapport à l’origine du repère.

La dérivée de la fonction $f$ est la fonction $f’$ définie sur $\mathbb{R}$ par $f’(x) = 3x^2$.

Pour tout $x\in \mathbb{R}$, $f’(x) \geq 0$ donc la fonction est croissante sur $\mathbb{R}$.
$f’(0) = 0$ donc la tangente à la courbe représentative de $f$ au point d’abscisse 0 est horizontale.

Propriétés :

• Les fonctions cosinus et sinus sont définies, continues et dérivables sur $\mathbb{R}$.
• Elles sont périodiques de période 2$\pi$ et leur représentation graphique est une sinusoïde de période 2$\pi$.
• Pour tout $x \in \mathbb{R}$, $\cos'(x) = -\sin(x)$ et $\sin'(x) = \cos(x)$.

Représentations graphiques :

• Fonction cosinus :

La fonction cosinus est paire donc elle est symétrique par rapport à l'axe des ordonnées.

• Fonction sinus :

La fonction sinus est impaire donc elle est symétrique par rapport à l'origine du repère.