Loi de Coulomb :
On se place dans le vide de permittivité absolue :
\[\rm E_0 = 8,854\cdot 10^{12}~F.m^{-1}\]
\[\boxed{\displaystyle \rm \frac{1}{4\pi\varepsilon_0} \approx 9\cdot 10^9 \Leftrightarrow \varepsilon_0 \approx \frac{1}{36\pi \cdot 10^9}}\]
D'après la 3ème loi de Newton, $\overrightarrow{\mathrm{F_{EIN}}} = -\overrightarrow{\mathrm{F_{NIE}}}$. Ce sont des forces électriques.
Dans un repère sphérique ayant pour origine le noyau, la loi de Coulomb donne :
$\boxed{\mathrm{\overrightarrow{F_{NIE}}} = + \frac{1}{4\pi\varepsilon_0}\frac{qq'}{r^2}\overrightarrow{\mathrm e_r}}$ avec $r = d \approx 145~\rm pm = 1,45 \cdot 10^{-\infty}~m$
Dans l'exemple du lithium, $q = -\rm e$, $q' = +\rm e$ donc $\overrightarrow{\mathrm{F_{NIE}}} = -\overrightarrow{\mathrm{F_{EIN}}} = \displaystyle\frac{1}{4π\varepsilon_0} \frac{\rm e^2}{r^2}\overrightarrow{\mathrm{\mathrm e{_r}}}$.
Champ électrique :
Par analogie avec l'intensité de la pesanteur $\vec{g}$ (ou champ de pesanteur), on peut définir un champ électrique $\overrightarrow{\rm E}$. Comme toute masse crée un champ de pesanteur (exemple de la Terre sur les objets qui nous entourent), toute charge crée un champ électrique $\overrightarrow{\rm E}$ qui attire ou repousse les charges à proximité.
Lorsque la charge $q'$ ne varie pas ou très peu et qu'elle est fixe dans le référentiel de l'observateur, on parle de champ électrostatique, champ électrique indépendant du temps.
On considère un tel champ et on suppose que $\parallel$ $\overrightarrow{\rm E}$ $\parallel = cste$.
Il ne dépend pas des coordonnées spatiales, il est donc uniforme.
Si la charge $q' > 0$, alors $\overrightarrow{\rm E}$ est selon $\overrightarrow{\mathrm e_r}$.
Si la charge $q' < 0$, alors $\overrightarrow{\rm E}$ est selon $-\overrightarrow{\mathrm e_r}$.
Champ uniforme constant :
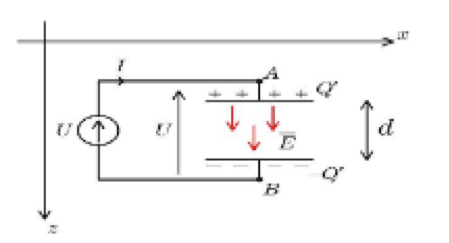
Un condensateur n’est pas juste un composant électronique. En régime continu, on peut accumuler des charges sur ses armatures, ces charges vont créer un tel champ qu’on pourra supposer constant.
$\boxed{\displaystyle \mathrm E = \frac{\rm U}{d}= \frac{\rm V_A - V_B}{d}}$ où $d$ est l'épaisseur du diélectrique.