Énergie mécanique
L'énergie mécanique notée $\rm E_m$, d'un corps est la somme de son énergie cinétique $\rm E_c$ et de son énergie potentielle de pesanteur $\rm E_{pp}$ :
\[\rm E_m = E_c + E_{pp}\]
On appelle énergie potentielle de pesanteur d'un solide $\rm S$ de masse m situé à l'altitude $z$ la quantité.
$\color{blue}{\boxed{\color{black}{\rm E_{pp} = m.g.z}}}$ avec $\scriptstyle \left\{\begin{array}{lll}
\scriptstyle\rm E_{pp} \text{ Energie potentielle de pensanteur en joules (J)}\\
\scriptstyle\rm m \text{ Masse du solide en kilogrammes (kg)}\\
\scriptstyle z \text{ Altitude du solide en mètres (m)}\\
\end{array}\right.$
Il existe deux types de forces s'appliquant sur un système, les forces conservatrices pour lesquelles l'énergie mécanique est conservée et les forces non conservatrices qui dissipent l'énergie mécanique du système.
|
Le travail d'une force conservatrice est égal à l'opposé de la variation d'énergie potentielle dont dérive cette force (théorème de l'énergie potentielle). $\color{black}{\delta\mathrm W = d\rm E_p}$ (TEP) |
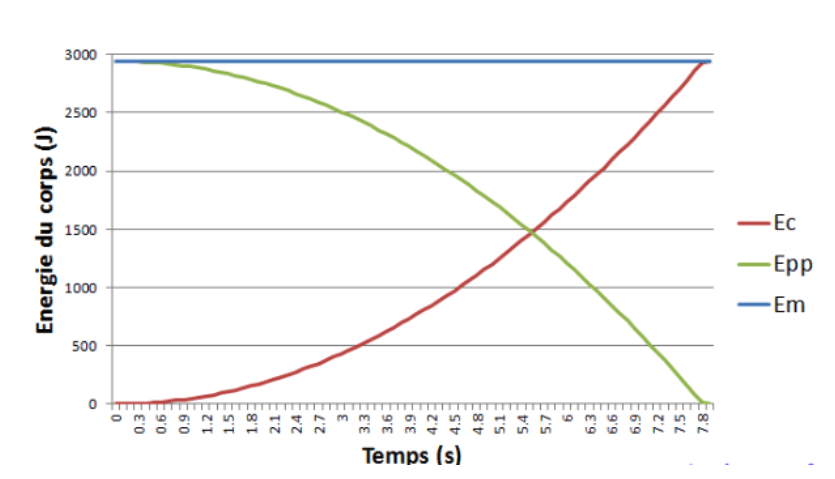
Conservation de l'énergie mécanique :
Au cours d'une chute sans frottement, l'énergie cinétique est constante : on dit qu'elle se conserve. La diminution de l'énergie potentielle de pesanteur est compensée par l'augmentation de l'énergie cinétique.