Un objet possède de l’énergie de position liée à son altitude.
Un objet en mouvement possède de l’énergie cinétique.
La somme de l’énergie cinétique et de l’énergie de position constitue l’énergie mécanique.
Lors de la chute d’un objet, l’augmentation de son énergie cinétique s’accompagne d’une diminution de son énergie de position.
Un objet de masse m et animé d’une vitesse v possède une énergie de mouvement, appelée énergie cinétique $\rm E_c$ :
\[\displaystyle \rm E_c = \frac{1}{2} \times m \times \mathcal v^2\]
Avec :
- La masse $\rm m$ est exprimée en kilogrammes $\rm (kg)$
- La vitesse $v$ exprimée en mètres par seconde $\rm (m/s)$
- L'énergie cinétique $\rm E_c$ exprimée en Joules $\rm (J)$
Théorème de l’énergie cinétique :
\[\displaystyle \rm E_c = \frac{1}{2} \times m \times \mathcal v^2\]
Avec :
- La masse m est exprimée en kilogrammes $\rm (kg)$
- La vitesse $v$ exprimée en mètres par seconde $\rm (m/s)$
- L'énergie cinétique $\rm E_c$ exprimée en Joules $\rm (J)$
La variation d'énergie cinétique $\rm E_c$ d'un solide entre $\rm A$ et $\rm B$ est liée au travail des forces appliquées entre $\rm A$ et $\rm B$ : c'est le théorème de l'energie cinétique :
$\rm E_{c_B}-E_{c_A} = \sum W_{AB}(\overrightarrow{F})$
$\displaystyle \frac{1}{2} \cdot m \cdot v_{\rm B}^2 - \frac{1}{2} \cdot m \cdot v_{\rm A}^2$ $\rm = \Delta E_c = \sum W_{AB}(\overrightarrow{F})$ avec $\rm A$ le point de départ et $\rm B$ le point d'arrivée.
On définit donc le moment d'inertie comme la somme des masses en chaque point du solide multiplié par la distance $r_1$ au carré des points à l'axe :
$\boxed{\displaystyle \mathrm J_\Delta = \sum^\infty_im_ir^2_i = \sum^\infty_im_i(\mathrm H_i \mathrm M_i)^2}$ (moment d'inertie en $\rm kg.m^2$)
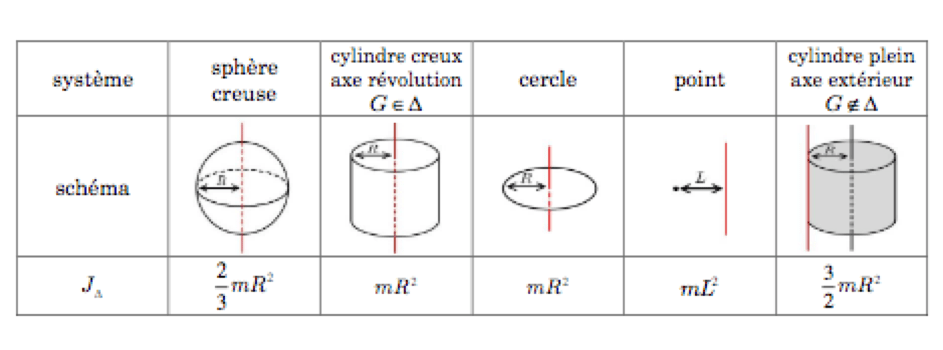
Moments d'inertie $\rm J_\Delta$ de quelques solides de géométrie simple :