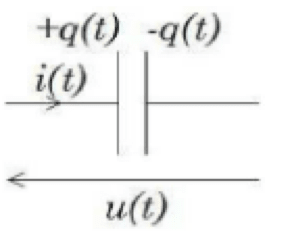En régime permanent, le condesateur bloque le passege du courant, les charges positives $+Q$ s'accumulant sur une plaque et les charges négatives $-Q$ s'accumulant sur l'autre plaque. Il se comporte comme un interrupteur ouvert (intensité nulle).
$\boxed{\scriptstyle q(t-\underset{\text{loi linéaire}}{=\mathrm C u_c} (t) \Rightarrow i_c (t) = \frac{dq(t)}{dt} = \mathrm C\frac{du_c(t)}{dt}}$ avec $\rm C$ capacité du condensateur en Farad $\rm (F)$.
Le condensateur stocke de l'énergie notée $\rm W_c(\mathcal t)$ (charges accumulées sur les armatures).
Et comme $\displaystyle p_c (t) = \frac{d\mathrm W_c(t)}{dt}$ alors : $\boxed{\mathrm W_c(t) = \frac{1}{2} \mathrm Cu^2_c(t)}$
Plus $\rm C$ est grand, plus l'énergie stockée par le condensateur à l'instant $t$ est grande donc $\rm C$ est la capacité d'un condensateur à accumuler de l'énergie.
En convention récepteur, cette énergie est strictement positive $(\rm C > 0)$ c'est-à-dire qu'elle est reçue du générateur par le condensateur puis restituée au circuit par la suite.