Calorimétrie

La matière est constituée d’un nombre trop grand d’entités (atomes, molécules, ions) pour que l’on puisse appliquer les lois physiques à l’échelle microscopique. On est donc obligé de décrire le comportement collectif d’un grand nombre d’espèces chimiques à l’aide de grandeurs physiques macroscopiques, mesurables à l’échelle humaine telles que la pression $\rm P$, le volume $\rm V$ ou la température $\rm T$. 

La constante d’Avogadro, notée $\rm N_A$, permet de faire le lien entre le réel à l’échelle microscopique et le réel tel qu’on l’appréhende, à l’échelle macroscopique. 

\[\color{pink}{\boxed{\color{black}{\rm N_A = 6,02 \times 10^{23}~mol^{-1}}}}\]

La température est une grandeur physique universelle. Cette mesure s’effectue avec un thermomètre gradué en degrés Celsius (noté $\rm °C$). Il existe d’autres unités de mesure : le degré Kelvin. 

\[\color{green}{\boxed{\color{blue}{\rm °C = K - 273}}}$

La quantité d’énergie est mesurée en Joule, ou J (et donc 1 kiloJoule, noté kJ, vaut 1000 Joules).

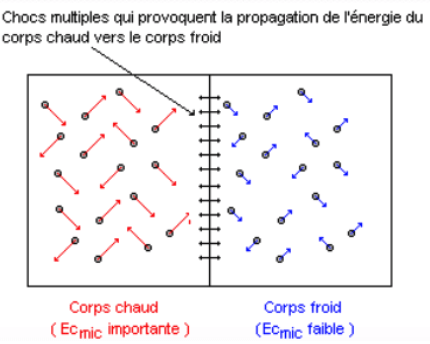
L'énergie interne U d'un système macroscopique est égale à la somme de : 

• L'énergie cinétique microscopique de chaque particule du système. Elle est fonction de l'agitation thermique, donc de la température ;
• L'énergie potentielle d'interactions microscopiques entre les particules dues aux interactions gravitationnelle, électromagnétique, forte et faible entre les particules du système.

\[\rm U = E_c(micro) + E_p(micro)\]

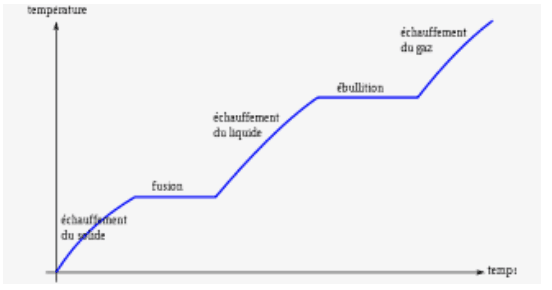
La capacité thermique $\rm C$ d’un corps condensé (solide ou liquide) correspond à l’énergie interne nécessaire pour augmenter sa température de $\rm 1°C$ sans le faire changer d’état physique. 

On utilise couramment la capacité thermique massique $c$ (en $\rm J.kg^{-1}.°C^{-1}$) et dans ce cas, on obtient la relation :

\[\rm \Delta U ~= ~m \times \mathcal c \times \Delta T\]

Plus la capacité thermique massique d’un corps est grande, plus ce corps refroidit ou réchauffe difficilement.
Ex : $c_{\rm Aluminium} = \rm 897~J.K^{-1}.kg^{-1}$ et $c_{\rm eau} = \rm 4,18 \cdot 10^3~J.K^{-1}.kg^{-1}$

Il faut beaucoup plus apporter d’énergie à l’eau pour la réchauffer. Par contre, celle-ci est un meilleur isolant car elle refroidira plus difficilement

Les transferts thermiques : 

 
Energie interne et température :

Lorsqu’un corps de masse $\rm m$, liquide ou solide, passe d’une température initiale $\rm T_I$ à une température finale $\rm T_F$, sa variation d’énergie interne $\rm \Delta U$ a pour expression :  

$\left.\begin{array}{lll}
\scriptstyle \rm \Delta U = m.\mathcal c.(T_F - T_I)\\
\boxed{\scriptstyle \rm \Delta U = m.\mathcal c.\Delta T}
\end{array}\right. \left|
\begin{array}{ll}
\scriptstyle \rm \Delta U \text{ en } J\\
\scriptstyle \rm \Delta T \text{ en kelvins (K) ou en °C}\\
\scriptstyle \rm m \text{ en kg}\\
\scriptstyle c \text{ en } \rm J.kg^{-1}.K^{-1}\text{ ou en } \\
\scriptstyle \rm J.kg^{-1}.°C^{-1}\\
\end{array}\right.$

La grandeur $c$ est appelée « capacité thermique massique » du solide ou du liquide en question. Elle représente l’énergie qu’il faut fournir pour augmenter de $\rm 1~K$ la température d’un kilogramme de ce solide ou liquide. 

Une transformation physique a lieu quand une espèce chimique passe d’un état physique (solide, liquide, gazeux) à un autre.

Attention ne pas confondre fusion et dissolution : lors de la fusion, l’espèce chimique passe de l’état solide à l’état liquide alors que lors de la dissolution, le sucre par exemple ne « fond » pas, il se dissout dans l’eau.

Les changements d’état d’un corps pur s’effectuent à une température constante sous une pression donnée.

Exemple d’équation d’un changement de l’eau : la vaporisation $\rm H_2O (l) \rightarrow H_2O (g)$.

On définit l’énergie massique de changement d’état L ou énergie latente de changement d’état en $\rm J.kg^{-1}$. L’énergie $Q$ transférée lors du changement d’état d’une masse d’une espèce est $Q = \rm m \times L$ avec $Q$ en $\rm J$ et $\rm m$ en $\rm kg$. 

Si $Q > 0$ alors transformation endothermique. Pour déterminer l’énergie massique de changement d’état, on utilise un calorimètre. Lors d’une fusion, une vaporisation ou une sublimation, l’énergie de l’espèce augmente et celle du milieu extérieur diminue (il se refroidit) : le transformation est endothermique.

Lors d’une solidification, une liquéfaction ou une condensation, l’énergie de l’espèce diminue et celle du milieu extérieur augmente (il se réchauffe) : la transformation est exothermique.