Fonctions exponentielles et logarithme décimal

Définition

Pour $a > 0$ fixé, la fonction exponentielle de base $a$ est la fonction $\exp_a : x \mapsto a^x$.

Elle est définie et positive sur $\mathbb{R}$   $\exp_a(0) = 1$.

Elle est dérivable sur $\mathbb{R}$ et :

• pour $0 < a < 1$, la fonction est décroissante sur $\mathbb{R}$.
• pour $a > 1$, la fonction est croissante sur $\mathbb{R}$.

Propriétés algébriques

Pour tous les $x$ et $y$ réels, et $n$ entier relatif :

$$a^{x + y} = a^x \times a^y \quad ; \quad a^{x - y} = \dfrac{a^x}{a^y} \quad ; \quad a^{nx} = (a^x)^n$$

Représentations graphiques selon les valeurs de $a > 0$

$0 < a = 0,3 < 1$   $a = 2 > 1$

Définition

Le logarithme décimal, noté $\log$, est la fonction définie sur $]0~;~+\infty[$ par :

Pour tout $b > 0$, $\log(b)$ est l'unique solution de $10^x = b$.

Pour $x > 0$ et $a$ réel : $\log(x) = a \Leftrightarrow x = 10^a$.

Elle est strictement croissante sur $]0~;~+\infty[$.

Propriétés algébriques

Valeurs particulières

$\log(1) = 0$ donc log est négative sur $]0~;~1]$ et positive sur $[1~;~+\infty[$.

$\log(10) = 1$.

Propriétés de calcul

Pour tout $a$ et $b$ réels strictement positifs, et $n \in \mathbb{N}$ :

• $\log(a \times b) = \log(a) + \log(b)$
• $\log\left(\dfrac{1}{b}\right) = -\log(b)$
• $\log\left(\dfrac{a}{b}\right) = \log(a) - \log(b)$
• $\log(a^n) = n\log(a)$

Pour $a = 10$ : $\log(10^n) = n\log(10) = n$.

Équation et inéquation

Équation : $\log(a) = \log(b) \Leftrightarrow a = b$

Inéquation : $\log(a) \leq \log(b) \Leftrightarrow a \leq b$

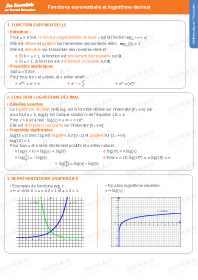
Représentation graphique