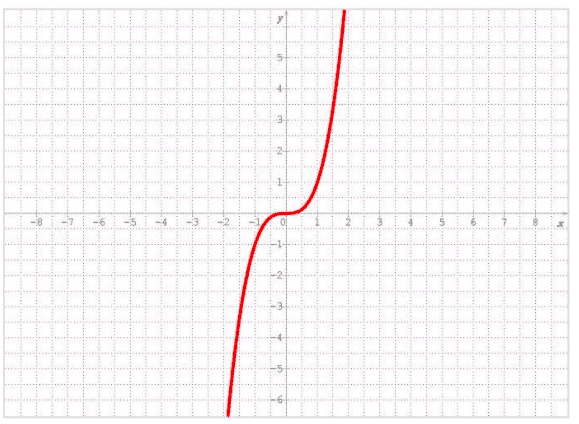
Fonction cube
Définition et domaine
La fonction cube ($x\mapsto x^3$) est définie et dérivable sur l'intervalle $]-\infty~; +\infty[$.
Dérivée et monotonie
Sur cet intervalle, sa dérivée est la fonction $x\mapsto 3x^2$ qui est strictement positive, sauf en $x = 0$. Elle est donc strictement croissante sur l'intervalle $]-\infty~; +\infty[$.
Propriétés géométriques
C'est une fonction impaire : sa représentation graphique est symétrique par rapport à l'origine du repère.