Définition
Pour $a > 0$ fixé, la fonction exponentielle de base $a$ est la fonction $\exp_a : x \mapsto a^x$.
Elle est définie et positive sur $\mathbb{R}$ $\exp_a(0) = 1$.
Elle est dérivable sur $\mathbb{R}$ et :
- pour $0 < a < 1$, la fonction est décroissante sur $\mathbb{R}$.
- pour $a > 1$, la fonction est croissante sur $\mathbb{R}$.
Propriétés algébriques
Pour tous les $x$ et $y$ réels, et $n$ entier relatif :
$$a^{x + y} = a^x \times a^y \quad ; \quad a^{x - y} = \dfrac{a^x}{a^y} \quad ; \quad a^{nx} = (a^x)^n$$
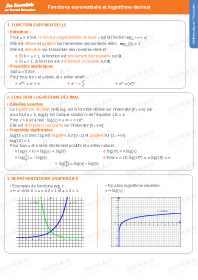
Représentations graphiques selon les valeurs de $a > 0$
$0 < a = 0,3 < 1$ $a = 2 > 1$