Géométrie

Théorème de Pythagore

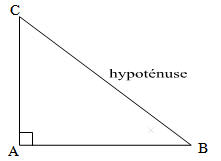
Dans le triangle $\rm ABC$ rectangle en $\rm A$, on a : ${\mathrm{BC}}^2 = {\mathrm{AB}}^2 + {\mathrm{AC}}^2$.

Le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.

Réciproque du théorème de Pythagore

Dans un triangle $\rm ABC$, si ${\mathrm{BC}}^2 = {\mathrm{AB}}^2 +{\mathrm{AC}}^2$, alors le triangle est rectangle en $\rm A$ et le segment $\rm [BC]$ est l'hypoténuse de ce triangle rectangle.

Théorème de Thalès

Énoncé du théorème

Soit A, M et B trois points alignés et A, N et C trois autres points alignés dans le même ordre.

Si les droites (BC) et (MN) sont parallèles, alors on a :

$$\frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC}$$

Configurations possibles

Il y a deux configurations possibles pour l'application du théorème de Thalès :

Aire des figures usuelles

Les aires des figures usuelles sont des formules fondamentales en géométrie qui permettent de calculer la surface de différentes formes géométriques. Ces formules sont essentielles pour résoudre de nombreux problèmes mathématiques et applications pratiques.

Formules principales

L'image présente les formules d'aire pour les figures géométriques les plus couramment utilisées en mathématiques. Chaque figure possède sa propre méthode de calcul basée sur ses dimensions caractéristiques.

Ces formules constituent la base du calcul d'aires en géométrie plane et sont indispensables pour la résolution d'exercices et de problèmes concrets impliquant des surfaces et des mesures.

Volume des figures usuelles

Les volumes des figures usuelles sont des formules fondamentales en géométrie qui permettent de calculer l'espace occupé par différents solides. Ces formules sont essentielles pour résoudre de nombreux problèmes mathématiques et applications pratiques.

Formules principales

Le tableau ci-dessus présente les formules de volume pour les principales figures géométriques tridimensionnelles. Chaque formule utilise des paramètres spécifiques selon la forme du solide considéré.

Ces formules de volume constituent un outil indispensable pour les calculs géométriques et sont largement utilisées dans les domaines scientifiques et techniques.