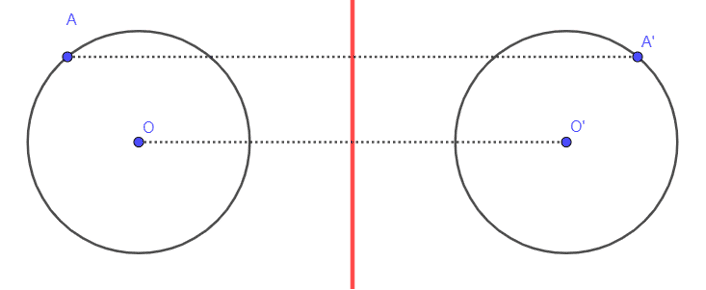
Safaanoo jàkkaarle (Symétrie)
Safaanoo jàkkaarle ci rëdd
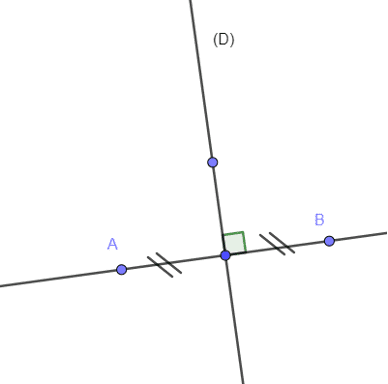
- Wax ne ñaari tomb $\rm A$ ak $\rm B$ da ñoo safaanoo jàkkaarle ci rëdd bii di $\bf (D)$ mu ngi firi ne $\rm (D)$ mooy xaaj-diggu dogit wii di $\rm [AB]$.
- Bépp tombu rëdd wii di $\rm (D)$ moom si boppam mooy safaanook jàkkaarleem ci $\bf (D)$.
Yeneen waxin
- Su $\rm A$ ak $\rm B$ safaanoo jàkkaarle ci bënn rëdd $\bf \Delta$, man na ñu wax tamit ne :
- $\rm B$ mooy safaanook jàkkaarle bu $\bf A$ ci $\bf \Delta$ wala itam $\rm A$ mooy safaanook jàkkaarle bu $\rm B$ ci $\Delta$.
- Su $\rm P$ nekkee bënn tomb bu rëdd wii di $\Delta$, konn safaanook jàkkaarle bu $\rm P$ mooy $\rm P$ si boppam.
- Tomb bu nekkul ci kow $\Delta$ safaanook jàkkaarleem da fay nekk « ci beneen wàllu » $\Delta$.
Nataalin
Nataalin : Soo bëggee nataal safaanook jàkkaarle bu bënn tomb wala bënn nataal, man nga jëfëndikoo bënn ekeer ak bënn reegal wu ñu maaskà wala bënn ekeer ak bënn kompa.
Ñaari nataal yu safaanoo jàkkaarle da ñuy yem kepp soo leen teglantee, waaye kènn ki dafay ëlbatiku ci wàllu keneen ki. Seen soreewaay ak rëdd wi ñu safaanoo jàkkaarle (ñu koy woowee aks) ñooy tolloo te seen ndëngin ci aks bòbu bënn la.
Ab nataal da fa safaanoo jàkkaarle su fekkee ne, soo ko lemee tey topp aksu safaanoo jàkkaarle bi, ñaari xaaji nataal wi d ñuy yemoo kepp. Ngir defar safaanook jàkkaarle bënn nataal, da ngay njëkka tek safaanook jàkkaarleek ay tomb yu bari ci nataal bòbu, soo noppee nga jokkale leen.

Safaanoo jàkkaarle yu nataal yu bari
Dogit
Safaanoo jàkkaarleeb bënn dogit ci bënn rëdd da fay nekk beneen dogit wu tollook moom guddaay.

Koñ (wala angal)
Safaanoo jàkkaarleeb bënn koñ (wala angal) da fay nekk beneen koñ bu tollook moom natt.

Ñetti tomb yu raŋale
Safaanoo jàkkaarleeb ñetti tomb yu raŋale ci bënn rëdd da ñuy nekk yeneen ñetti tomb yu raŋale.

Mbege
Safaanoo jàkkaarleeb bënn mbege ci bënn rëdd da fay nekk bënn mbege bu tollook moom ceñeer.