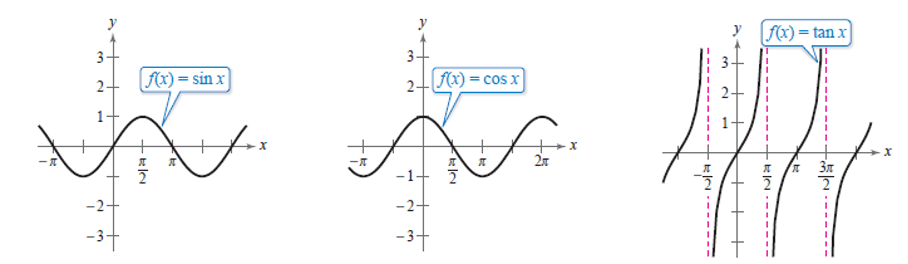1) Dans les tableaux ci-dessous, on récapitule les propriétés des fonctions trigonométriques. (On pourra les retrouver à l’aide d’un cercle trigonométrique).
$\begin{array}{|clc|} \hline \cos ^2 x+\sin ^2 x=\color{cornflowerblue}{1}& \\ \hline \tan x= & \color{cornflowerblue}{\dfrac{\sin x}{\cos x}} \\ \hline \operatorname{cotan} x= & \color{cornflowerblue}{\dfrac{\cos x}{\sin x}} \\ \hline \end{array}$
$\begin{array}{|cl|} \hline 1+\tan ^2 x= & \color{cornflowerblue}{\dfrac{1}{\cos ^2 x}} \\ \hline 1+\operatorname{cotan}^2 x= & \color{cornflowerblue}{\dfrac{1}{\sin ^2 x}} \\ \hline \end{array}$
$\begin{array}{|c|c|c|c|c|c|} \hline x & 0 & \dfrac{\pi}{6} & \dfrac{\pi}{4} & \dfrac{\pi}{3} & \dfrac{\pi}{2} \\ \hline \cos x & \color{cornflowerblue}{1} & \color{cornflowerblue}{\dfrac{\sqrt{3}}{2}} & \color{cornflowerblue}{\dfrac{\sqrt{2}}{2}} & \color{cornflowerblue}{\dfrac{1}{2}} & \color{cornflowerblue}{0} \\ \hline \sin x & \color{cornflowerblue}{0} & \color{cornflowerblue}{\dfrac{1}{2}} & \color{cornflowerblue}{\dfrac{\sqrt{2}}{2}} & \color{cornflowerblue}{\dfrac{\sqrt{3}}{2}} & \color{cornflowerblue}{1} \\ \hline \tan x & \color{cornflowerblue}{0} & \color{cornflowerblue}{\dfrac{1}{\sqrt{3}}} & \color{cornflowerblue}{1} & \color{cornflowerblue}{\sqrt{3}} & \begin{array}{c} \color{cornflowerblue}{\text { Non } \\ \text { Définie}} \end{array} \\ \hline \end{array}$
$\begin{array}{|c|c|c|c|c|c|c|}
\hline x & x+2 \pi & -x & x+\pi & \pi-x & x+\dfrac{\pi}{2} & \dfrac{\pi}{2}-x \\
\hline \cos x & \color{cornflowerblue}{\cos x} & \color{cornflowerblue}{\cos x} & \color{cornflowerblue}{-\cos x} & \color{cornflowerblue}{-\cos x} & \color{cornflowerblue}{-\sin x} & \color{cornflowerblue}{\sin x} \\
\hline \sin x & \color{cornflowerblue}{\sin x} & \color{cornflowerblue}{-\sin x} & \color{cornflowerblue}{-\sin x} & \color{cornflowerblue}{\sin x} & \color{cornflowerblue}{\cos x} & \color{cornflowerblue}{\cos x} \\
\hline \tan x & \color{cornflowerblue}{\tan x} & \color{cornflowerblue}{-\tan x} & \color{cornflowerblue}{\tan x} & \color{cornflowerblue}{-\tan x} & \color{cornflowerblue}{-\operatorname{cotan} x} & \color{cornflowerblue}{\operatorname{cotan} x} \\
\hline
\end{array}$
$\sin x=\sin a$ si et seulement si :
$\color{cornflowerblue}{x=a+2 k \pi \textbf{ ou } x=\pi-a+2 k \pi.}$ $\color{cornflowerblue}{\quad(k \in \mathbb{Z})}$
$\cos x = \cos a$ si et seulement si :
$\color{cornflowerblue}{x=a+2 k \pi \textbf{ ou } x=-a+2 k \pi.}$ $\color{cornflowerblue}{\quad(k \in \mathbb{Z})}$
$\tan x=\tan a$ si et seulement si :
$\color{cornflowerblue}{x=a+k \pi.}$ $\color{cornflowerblue}{\quad (k \in \mathbb{Z})}$
$\begin{array}{|l|} \hline \cos (x+y)=\color{cornflowerblue}{\cos x \cos y-\sin x \sin y} \\ \hline \sin (x+y)=\color{cornflowerblue}{\sin x \cos y+\cos x \sin y} \\ \hline \cos (x-y)=\color{cornflowerblue}{\cos x \cos y+\sin x \sin y} \\ \hline \sin (x-y)=\color{cornflowerblue}{\sin x \cos y-\cos x \sin y} \\ \hline \tan (x+y)=\color{cornflowerblue}{\dfrac{\tan x+\tan y}{1-\tan x \tan y}} \\ \hline \tan (x-y)=\color{cornflowerblue}{\dfrac{\tan x-\tan y}{1+\tan x \tan y}} \\ \hline\end{array}$
$\begin{array}{|ll|} \hline \scriptstyle{(1)}& \cos 2 x= & \color{cornflowerblue}{\cos ^2 x-\sin ^2 x} \\ \hline \scriptstyle{(2)}& \cos 2 x= & \color{cornflowerblue}{2 \cos ^2 x-1} \\ \hline \scriptstyle{(3)}& \cos 2 x= & \color{cornflowerblue}{1-2 \sin^2 x} \\ \hline & \sin 2 x= & \color{cornflowerblue}{2 \sin x \cos x} \\ \hline & \tan 2 x= & \color{cornflowerblue}{\dfrac{2 \tan x}{1-\tan x \tan y}} \\
\hline\end{array}$
2) On pose : $\tan \dfrac{x}{2}=t$. Exprimer en fonction de $t$ : $\cos x$, $\sin x$ et $\tan x$.
Si $\tan\dfrac{x}{2} = t$, on a :
$\begin{array}{|c|c|c|} \hline \cos x=\color{cornflowerblue}{\dfrac{1-t^2}{1+t^2}} & \sin x=\color{cornflowerblue}{\dfrac{2 t} {1+t^2}} & \tan x=\color{cornflowerblue}{\dfrac{2 t}{1-t^2}} \\ \hline \end{array}$
3) Formules de linéarisation et de factorisation
$\begin{array}{|c|}\hline \sin a \cdot \cos b=\color{cornflowerblue}{\dfrac{1}{2}[\sin (a+b)+\sin (a-b)]} \\ \cos a \cdot \cos b=\color{cornflowerblue}{\dfrac{1}{2}[\cos (a+b)+\cos (a-b)]} \\ \hline \sin a \cdot \sin b=\color{cornflowerblue}{\dfrac{1}{2}[\cos (a-b)-\cos (a+b)]} \\ \hline \end{array}$
$\begin{array}{|c|}\hline \sin p+\sin q=\color{cornflowerblue}{2 \sin \dfrac{p+q}{2} \cos \dfrac{p-q}{2}} \\ \hline \sin p-\sin q=\color{cornflowerblue}{2 \cos \dfrac{p+q}{2} \sin \dfrac{p-q}{2}} \\
\hline \cos p+\cos q=\color{cornflowerblue}{2 \cos \dfrac{p+q}{2} \cos \dfrac{p-q}{2}} \\ \hline \cos p-\cos q=\color{cornflowerblue}{-2 \sin \dfrac{p+q}{2} \sin \dfrac{p-q}{2}} \\ \hline \end{array}$
4) Études des fonctions trigonométriques
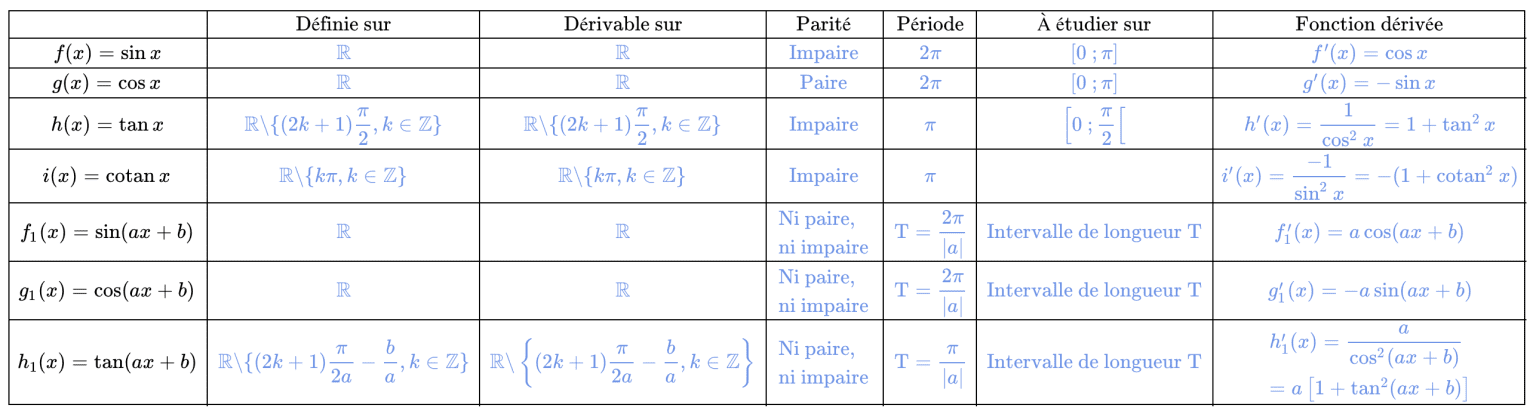
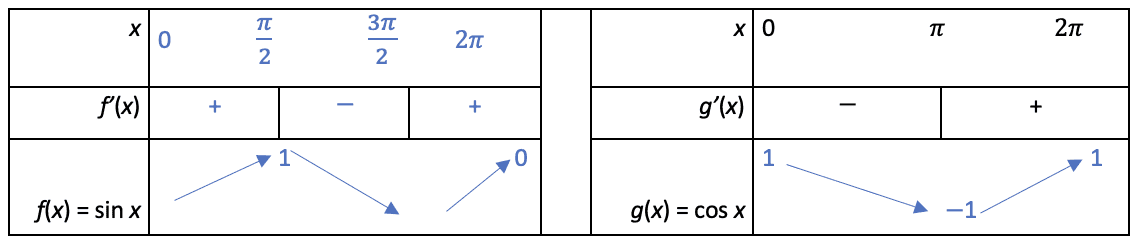
a. Tableaux de variations sur $[0~;2\pi]$ :
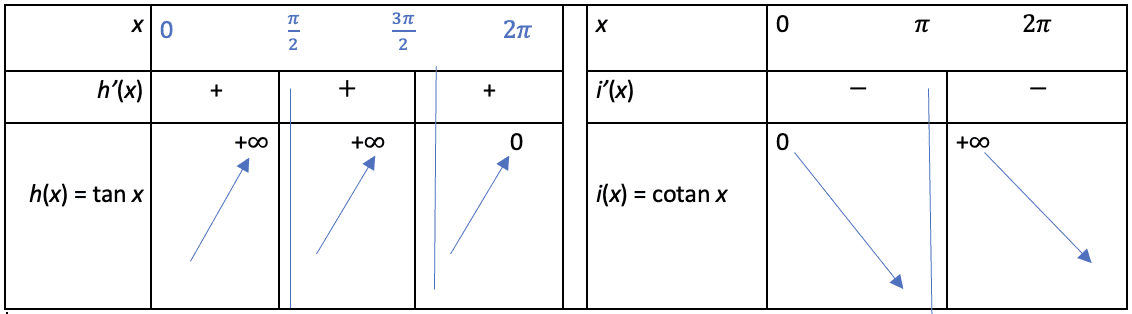
b. Courbes :