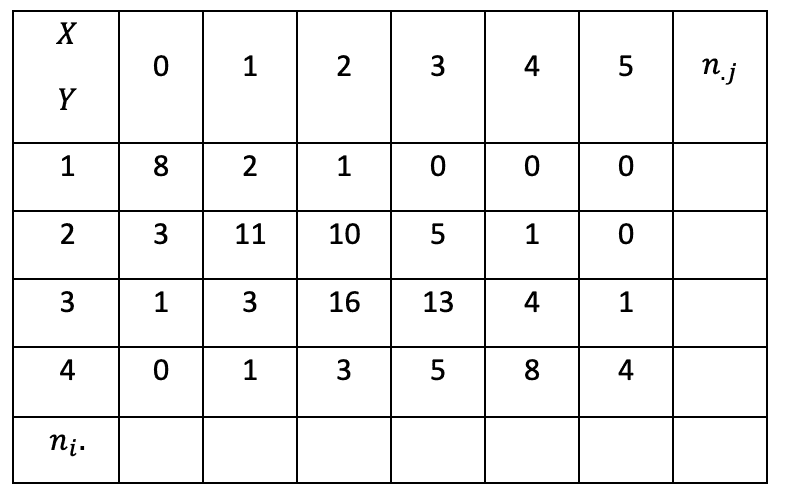
Notion d’ajustement
Un nuage représentant une série statistique double peut avoir différents aspects.
Ajuster un nuage par une courbe, c'est trouver la courbe la « plus proche » des points du nuage.
Cette courbe est appelée courbe d’ajustement ou de régression ou d’estimation. Si cette courbe est une droite, on parle de régression linéaire.
Ajustement linéaire par la méthode des moindres carrées
On considère le nuage de $n$ points $\mathrm A_i\left(x_i y_i\right)$, $1 \leq i \leq n$ d'effectifs tous égaux à 1, représentant une série statistique double $\rm (X, Y)$.
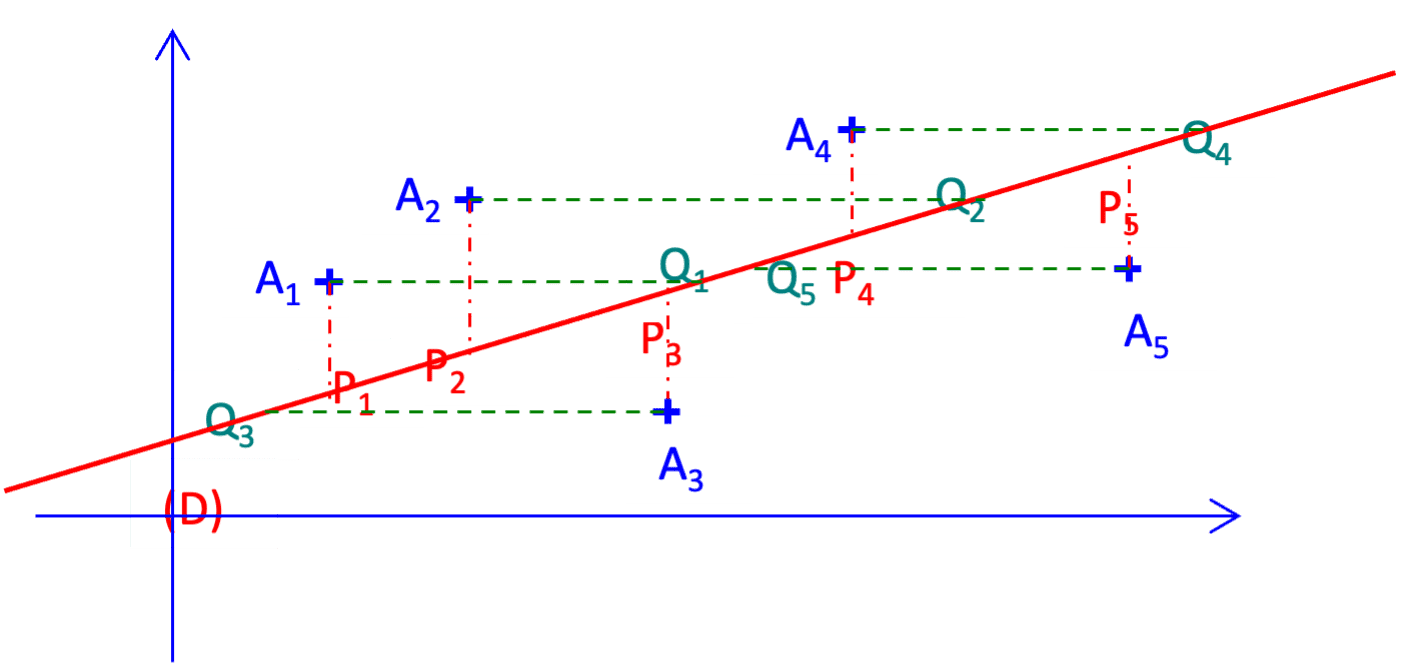
Essayons d'approcher ce nuage par une droite $\rm (D)$.
Supposons que les points ne sont pas tous situés sur une droite parallèle à l'axe des ordonnées, c'est-à-dire, $\rm X$ n'est pas une constante. On désigne par $\mathrm P_i$ le projeté de $\mathrm A_i$ sur la droite $\rm (D)$ parallèlement à l'axe des ordonnées.
Supposons que les points ne sont pas tous situés sur l'axe des ordonnées, c'est-à-dire, $\rm Y$ n'est pas une constante. On désigne $\mathrm Q_i$ le projeté de $\mathrm A_i$ sur la droite $\rm (D)$ parallèlement à l'axe des abscisses.
La méthode des moindres carrés consiste à chercher une droite $\rm (D)$ d'équation $y=a x+b$ qui rend minimale la somme des $\mathrm A_i \mathrm P_i^2$ ou une droite d'équation $x=a^{\prime} y+b^{\prime}$ qui rend minimale la somme des $\mathrm A_i \mathrm Q_i{ }^2$.
$\mathrm{P}_i \mathrm{A}_i^2=\left(y_i-a x_i-b\right)^2$ ou $\mathrm A_i \mathrm{Q}_i^2=\left(x_i-a^{\prime} y_i-b^{\prime}\right)^2$.
Dans le premier cas, $\rm (D)$ est appelée droite de régression de $\rm Y$ en $\rm X$. On la note $\rm D_{Y / X}$.
Dans le deuxième cas, $\rm (D)$ est appelée droite de régression de $\rm X$ en $\rm Y$. On la note $\rm D_{X / Y}$.
Définition : Soit $\bar{x}$ et $\bar{y}$ les moyennes des séries marginales associées à la série double $\rm (X, Y)$ d'effectif $\rm N$. On appelle covariance de $\rm (X, Y)$ le réel noté $\operatorname{cov}\rm (X, Y)$ ou $\sigma_{X Y}$ défini par :
$\operatorname{cov}(\mathrm{X}, \mathrm{Y})=\dfrac{n_{11} x_1 y_1+n_{12} x_1 y_2+\ldots+n_{pq} x_p y_q}{\mathrm{N}}-\overline{xy}$
Remarques : $\operatorname{cov}(\mathrm{X}, \mathrm{X})=\mathrm{V}(\mathrm{X}) ; \operatorname{cov}(\mathrm{Y}, \mathrm{Y})=\mathrm{V}(\mathrm{Y})$
Théorèmes :
- La droite de régression de $\rm Y$ en $\rm X$ passe par le point moyen et a pour équation :
$\boxed{y-\bar{y} = a(x-\bar{x})}$ avec $a=\dfrac{\operatorname{cov}(\mathrm{X}, \mathrm{Y})}{\mathrm{V}(\mathrm{X})}$
- La droite de régression de $\rm X$ en $\rm Y$ passe par le point moyen et a pour équation :
$\boxed{x-\bar{x}=a^{\prime}(y-\bar{y})}$ avec $a^{\prime}=\dfrac{\operatorname{cov}(\mathrm{X}, \mathrm{Y})}{\mathrm{V}(\mathrm{Y})}$
Remarque : Ces équations permettent de trouver par extrapolation à partir d'une valeur de $x$ fixée, la valeur de $y$ estimée et inversement.
Coefficient de corrélation linéaire
Lorsque les points du nuage sont groupés « en gros » suivant une direction rectiligne, on a une dépendance statistique linéaire entre les caractères $\rm X$ et $\rm Y$. On dit qu'il $y$ a corrélation linéaire entre $\rm X$ et $\rm Y$.
Définition :
On appelle coefficient de corrélation linéaire d'une série statistique double $(\mathrm{X} ; \mathrm{Y})$ le réel $r$ défini par :
$r=\dfrac{\operatorname{COV}(\mathrm{X} ; \mathrm{Y})}{\sqrt{\mathrm{V}(\mathrm{X}) \mathrm{V}(\mathrm{Y})}}$ ou $r=\dfrac{\operatorname{COV}(\mathrm{X} ; \mathrm{Y})}{\sigma_{\mathrm{X}} \sigma_{\mathrm{Y}}}$
Propriétés :
- On a $r^2=aa^{\prime}$ où $a$ et $a^{\prime}$ sont les coefficients directeurs respectifs des droites de régression de $\rm Y$ en $\rm X$ et de $\rm X$ en $\rm Y$.
- On a toujours : $-1 \leq r \leq 1$
Remarque :
Si $a < 0$ et $a^{\prime}<0$ alors $r=-\sqrt{aa}$
Si $a > 0$ et $a^{\prime}>0$ alors $r=\sqrt{a a^{\prime}}$
Appréciation de la corrélation linaire :
Le réel $|r|$ permet d’apprécier la corrélation linéaire entre les variables $\rm X$ et $\rm Y$.
Si $0,87 \leq |r| \leq 1$ alors la corrélation linéaire entre les deux variables est forte.
Si $|r| < 0,87$ la corrélation est faible.
Remarque : si la corrélation est faible, un ajustement linéaire n’est pas justifié.