Oscillations mécaniques libres

📝 Mini-cours GRATUIT

Je m’inscris pour accéder gratuitement à ce contenu

Oscillations mécaniques libres

Oscillations mécaniques libres non amorties

Exemple du pendule élastique horizontale

Équation différentielle du mouvement :

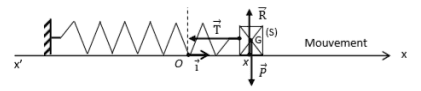
$TCI$ : $\overrightarrow{p}+\overrightarrow{R}+\overrightarrow{T}=\overrightarrow{ma}$ suivant $(O,\overrightarrow{i})$ : $0+0-Kx=mx\Longleftrightarrow \ddot x + \dfrac{k}{m}x=0$

$\ddot x + \omega_0^2 x =0$ avec $\omega_0^2=\dfrac{k}{m}$

$\omega_0 = \sqrt{\frac{k}{m}}$ Pulsation propre de l'oscillateur.

Solution de l'équation différentielle :

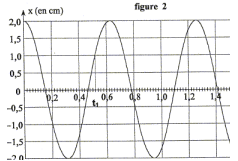
Elle est de la forme : $x=X_mcos(w_ot+\varphi)$

Ou $x=X_msin(w_ot+\varphi)$

Caractéristiques du mouvement
- Pulsation propre $\omega$ : $\omega_0 = \sqrt{\frac{k}{m}}$

- Période propre $T_0$ : $T_0=\frac{2\pi}{\omega_0}=2\pi\sqrt{\frac{m}{k}}$
- Fréquence propre $N_0$ : $N_0=\frac{1}{T_0}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$

Équations horaires

Équation horaire du mouvement :

$x=X_mcos(w_ot+\varphi)$ ou $x=X_msin(w_ot+\varphi)$

avec $-X_m\le x \le X_m$
où $X_m=$ élongateur maximal ou amplitude

Équation horaire de la vitesse :

$V=\dfrac{dx}{dt}=\dot x = -X_m \omega_0 sin(w_ot+\varphi)$

NB: $V_{max}=X_m\omega_0$et V est maximale au point $x=0$

Équation horaire de l'accélération :

$a=\ddot x = -X_m\omega_0^2 cos(w_ot+\varphi)$

NB : $a_{max}=X_m\omega_0^2$

Étude énergétique

L'énergie mécanique du système {ressort, poulie} est $E_m=E_c+E_p=\dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2=\dfrac{1}{2}kX_m^2=cste$

L'énergie mécanique d'une oscillation non amortie est constante : On dit qu'elle se conserve.

Oscillations mécaniques libres amorties

Équation differentielle du mouvement

$\ddot x + \dfrac{h}{m}\dot x + \frac{k}{m}x=0$
Avec $h=$ coefficient de frottement.

On distingue trois régimes d'oscillations :

Si $h$ est faible $(h < \sqrt{\dfrac{2k}{m}})$, on a le régime pseudo périodique.
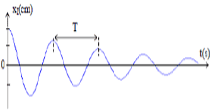
Si $h$ est élevé $(h > \sqrt{\dfrac{2k}{m}})$, on a le régime apériodique.
Si $h$ est moyen $(h=\sqrt{\dfrac{2k}{m}})$, on a le regime critique.