I. Oscillations électriques libres non amorties
Définition
Un circuit oscillant est un circuit électrique constitué d’un condensateur de capacité $C$ et d’inductance $L$ et de résistance négligeable
Équation différentielle de la décharge du circuit

Loi des mailles
$$u_c-u_L=0 \Rightarrow \frac{q}{C}+L\frac{di}{dt}=0 \Rightarrow L\ddot q + \frac{q}{C}=0 \Rightarrow \ddot q + \frac{q}{LC}=0$$
Charge instantanée dans le circuit
La charge $q$ est la solution de l’équation différentielle. La solution est $q=Q_m \cos(\omega_0 t + \varphi)$ où $\varphi$ est la phase à l’origine, $\omega_0$ est la pulsation propre et $Q_m$ est la valeur maximale de la charge
Caractéristiques du circuit
- Pulsation propre
La pulsation propre est $\omega_0^2=\dfrac{1}{\sqrt{LC}} \Rightarrow \omega_0 = \sqrt{\dfrac{1}{LC}}$.
L’unité de la pulsation propre est $\rm rad.s^{-1}$
- Période propre
Par définition $T_0 = \frac{2\pi}{\omega_0} \Rightarrow T_0 = 2\pi \sqrt{LC}$. L’unité de la période propre est la seconde ($s$)
- Fréquence propre
La fréquence $N_0 = f_0 = \dfrac{1}{T_0} \Rightarrow f_0 = \dfrac{1}{2\pi\sqrt{LC}}$. L’unité de la fréquence et le Hertz ($Hz$)
Étude énergétique
- Énergie électromagnétique emmagasinée dans le circuit
Énergie électrique dans le condensateur :
$E_c = \dfrac{1}{2}\dfrac{q^2}{C}$
Énergie magnétique dans la bobine :
$E_m = \dfrac{1}{2}Li^2$
Énergie électromagnétique :
$E = E_c + E_m \Rightarrow E = \dfrac{1}{2}\dfrac{q^2}{C} + \dfrac{1}{2}Li^2$
- Conservation de l’énergie totale dans le circuit
On a $q=Q_m \cos(\omega_0 t + \varphi)$ et $i=\dfrac{dq}{dt} \Rightarrow i=-Q_m\omega_0 \sin(\omega_0 t + \varphi)$
$E = \dfrac{1}{2}\dfrac{q^2}{C} + \dfrac{1}{2}Li^2$
$\Rightarrow E = \dfrac{1}{2}\dfrac{Q_m^2 \cos^2(\omega_0 t + \varphi)}{C} + \dfrac{1}{2}L Q_m^2 \omega_0^2 \sin^2(\omega_0 t + \varphi)$
$\Rightarrow E = \dfrac{1}{2}\frac{Q_m^2}{C} \cos^2(\omega_0 t + \varphi) + \dfrac{1}{2}L\dfrac{Q_m^2}{LC} \sin^2(\omega_0 t + \varphi)$
$\Rightarrow E = \dfrac{1}{2}\dfrac{Q_m^2}{C} (\cos^2(\omega_0 t + \varphi) + \sin^2(\omega_0 t + \varphi))$
$\Rightarrow E = \dfrac{1}{2}\frac{Q_m^2}{C}$
L’énergie totale du circuit oscillant est constante car $Q_m$ et $C$ sont des constantes.
Analogie entre oscillations mécaniques et oscillations électriques libres
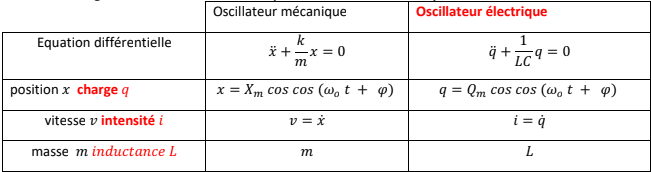

II. Oscillations électriques libres amorties
Équation différentielle
| Loi des mailles $u_C-u_L-u_R=0$ $\Rightarrow \dfrac{q}{C} + r i + L\dfrac{di}{dt}+Ri = 0$$\Rightarrow L\ddot q + R_Ti+\dfrac{q}{C}=0$ $\Rightarrow L\ddot q+ R_T \dfrac{dq}{dt} + \dfrac{q}{C}=0$ |
Différents régimes
- Si la résistance totale $R_T$ est faible : on a le régime pseudo-périodique où l’amplitude des oscillations diminue progressivement avant de s’annuler
- Si la résistance totale $R_T$ est élevée : on a un régime apériodique où l’amplitude des oscillations s’annule directement sans osciller
- Si la résistance totale $R_T$ est égale à la résistance critique $R_c = 2\sqrt{\dfrac{L}{C}}$, on a le régime critique où l’amplitude s’annule pendant la durée la plus courte.
Étude énergétique
$E = E_c + E_L \Rightarrow E = \dfrac{1}{2}Li^2 + \dfrac{1}{2}\dfrac{q^2}{C}$ $\Rightarrow \dfrac{dE}{dt} = \dfrac{q\dot q}{C} + (Li \dfrac{di}{dt}=\dfrac{q}{C}q+L\dot q\ddot q$
$\Rightarrow \dfrac{dE}{dt}=\dot q\left(L\ddot q + \dfrac{q}{C}\right)$
Or $L\ddot q + \dfrac{q}{C} = - R_ti$, $\dfrac{dE}{dt} = \dot q(-R_t i)= -R_T\dot q^2=-R_Ti^2 < 0$
L’énergie diminue au cours du temps à cause de la résistance $R_T$ (effet Joule).


