1. Les niveaux d'énergie de l'atome
Hypothèses de Niels Bohr
- Tout atome possède une énergie $E$ telle que celle-ci ne peut prendre que certaines valeurs formant une suite discontinue : On dit qu'elle est quantifiée. Les états énergétiques correspondant à ces valeurs particulières sont appelés niveaux d'énergie de l'atome.
- Le passage d'un niveau d'énergie à un autre est appelé transition électronique.
Transition électronique
- Une transition électronique est le passage d'un atome, d'un niveau d'énergie à un autre. Une transition électronique entre deux niveaux d'énergie $E_p$ et $E_n$ ne peut se faire que par absorption ou émission d'un photon de fréquence $v_{np}$ : Les variations d'énergie de l'atome sont quantifiées
- Émission d'un photon
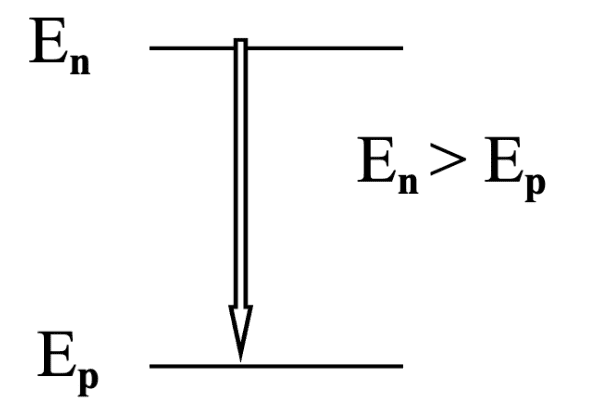
$E=hv_{np} \rightarrow$ L’énergie d’un photon émis est égal à l’énergie de la transition électronique réalisée.
- Absorption d'un photon
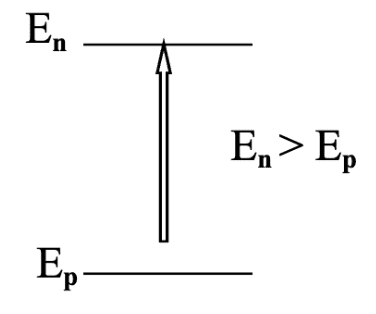
$E=hv_{np} \rightarrow$ L’énergie du photon absorbé est égal à l’énergie de la transition qu’il permet de réaliser.
- Excitation - désexcitation - ionisation
Si $E_p$ correspond à l’état fondamental (état de plus basse), les états $E_n > E_p$ correspond aux états excités :
- Une transition $E_p \rightarrow E_n$ correspond à une excitation (l’atome absorbe un photon $h\nu_{np}$ et se met dans un état excité).
- Une transition $E_n \rightarrow E_p$ est une désexcitation (l’atome émet un photon $h\nu_{np}$ et revient à son état fondamental).
- Une ionisation correspond au passage de l’atome du niveau $E_p$ à l’infini (l’atome se transforme en ion).
2. Application à l'atome d'hydrogène
Niveaux d'énergie
- Expression
- À l'état fondamental, l'électron d'un atome d'hydrogène se situe dans la couche K ($n=1$). Dans les états excités, l'électron se place dans l'une des couches L ($n=2$), M ($n=3$) etc ...
- À chacun de ces états, il correspond un niveau d'énergie d'ordre $n$ avec $E_n = \dfrac{-E_0}{n^2}$ avec $E_0 = 13,6 \text{ eV}$ et $n =$ nombre quantique principal (numéro de la couche).
- Énergie d'ionisation : C'est l'énergie minimale qu'il faut fournir à l'atome d'hydrogène dans son état fondamental pour lui arracher son électron. $H^+$ ($n=\infty$ $E_\infty =0$)
$E_1= \text{énergie d'ionisation} = (E_\infty - (-E_0)) = + E_0$
$E_i = E_0 = +13,6 \text{ eV} = 2,18 \cdot 10^{-18} \text{ J}$
Spectre atomique de l'hydrogène
Lors d'une transition du niveau $E_n$ à un niveau inférieur $E_p$, un photon de fréquence $v_{np}$ (de longueur d'onde $\lambda_{np} = \dfrac{c}{v_{np}}$ et d'énergie $E= hv_{np} (E_n- E_p)$
- Fréquence du photon émis : $v_{np} = \dfrac{E}{h} = \dfrac{(E_n- E_p)}{h} = \dfrac{E_0}{h}(\dfrac{1}{p^2}-\dfrac{1}{n^2})$
- Longeur d'onde du photon émis : $v_{np} = \dfrac{c}{\lambda_{np}} = \dfrac{E_0}{h}(\dfrac{1}{p^2}-\dfrac{1}{n^2}) \implies \dfrac{1}{\lambda_{np}} = \dfrac{E_0}{hc}(\dfrac{1}{p^2}-\dfrac{1}{n^2}) \implies \dfrac{1}{\lambda_{np}} = R_H(\dfrac{1}{p^2}-\dfrac{1}{n^2})$ avec $R_H = \dfrac{E_0}{hc} = 1,097 \cdot 10^7 \text{ m}^{-1}$ est appelé constante de Rydberg $\implies \dfrac{1}{\lambda_{np}} = R_H(\dfrac{n^2 - p^2}{n^2p^2}) \implies \lambda_{np} = (\dfrac{n^2p^2}{n^2 - p^2})\dfrac{1}{R_H}$
Séries des raies d'émission
- Série de Lyman :
Si $p =1$ et $n = 2, 3, 4......$
Toutes les transitions aboutissent au niveau fondamental : c'est la série de Lyman.
-
- les fréquences de Lyman : $v_{n1} = (\dfrac{1}{1^2}-\dfrac{1}{n^2})\dfrac{E_0}{h}$
- les longueurs d'onde de Lyman $\dfrac{1}{\lambda_{n1}} = R_H(\dfrac{1}{1^2}-\dfrac{1}{n^2}) \implies \lambda_{np} = (\dfrac{n^2}{n^2 - 1})\dfrac{1}{R_H}$
- longueur d'onde limite de Lyman : si $n$ tend vers $\infty$ $\implies \lambda_l = \dfrac{hc}{E_0} = \dfrac{1}{R_H}$
- Série de Balmer :
Si $p= 2$ et $n= 3, 4, 5...$
Les transitions aboutissent au niveau $n= 2$ et constituent la série de Balmer- les fréquences de Balmer : $v_{n1} = (\dfrac{1}{2^2}-\dfrac{1}{n^2})\dfrac{E_0}{h}$
- les longueurs d'onde de Balmer : $\dfrac{1}{\lambda_{n1}} = R_H(\dfrac{1}{2^2}-\dfrac{1}{n^2}) \implies \dfrac{1}{\lambda_{np}} = \dfrac{R_H}{4}(\dfrac{n^2 - 4}{n^2}) \implies \lambda_{np} = \dfrac{4}{R_H}(\dfrac{n^2}{n^2 - 4})$
- longueur d'onde limite de Balmer : si $n$ tend vers $\infty$ $\implies \lambda_l = \dfrac{4hc}{E_0} = \dfrac{4}{R_H}$
- longueur d'onde limite (qd $n \rightarrow +\infty$) : $\lambda_1 = 364,4 \text{ nm}$
- Série de Paschen :
Les transitions aboutissent au niveau $n= 3$ et constituent la série de Paschen.- les fréquences de Paschen : $v_{n1} = (\dfrac{1}{3^2}-\dfrac{1}{n^2})\dfrac{E_0}{h}$
- les longueurs d'onde de Paschen : $\dfrac{1}{\lambda_{n1}} = R_H(\dfrac{1}{3^2}-\dfrac{1}{n^2}) \implies \dfrac{1}{\lambda_{np}} = \dfrac{R_H}{9}(\dfrac{n^2 - 9}{n^2}) \implies \lambda_{np} = \dfrac{9}{R_H}(\dfrac{n^2}{n^2 - 9})$
- longueur d'onde limite de Paschen : si $n$ tend vers $\infty$ $\implies \lambda = \dfrac{9hc}{E_0} = \dfrac{9}{R_H}$
- longueur d'onde limite : $\lambda_l = 819,9 \text{ nm}$.
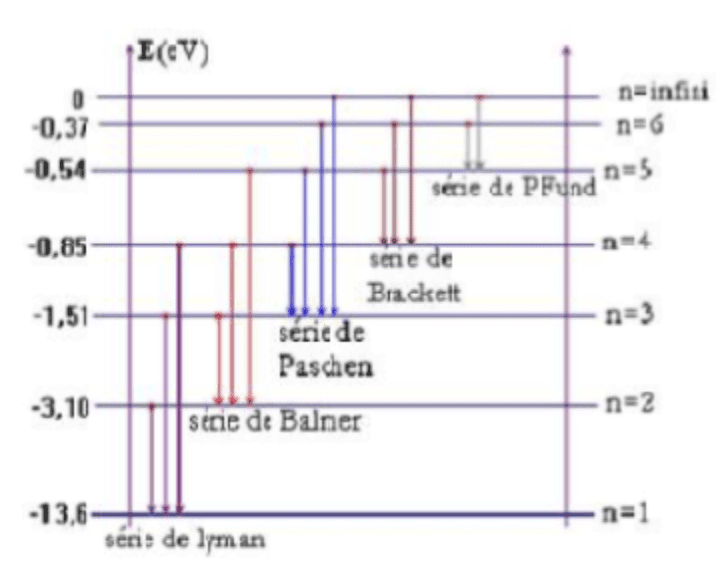
Série des raies d'émission de l'atome d'hydrogène


