Interférences lumineuses

1. Interférences en lumière monochromatique

Mise en évidence du phénomène :

• Dispositif expérimental : les fentes de Young :
  • $S$ source de lumière monochromatique
  • Les fentes $S_1$ et $S_2$, très proches l'une de l'autre, sont des sources secondaires
  • Les deux faisceaux diffractés se superposent sur un écran $E$.

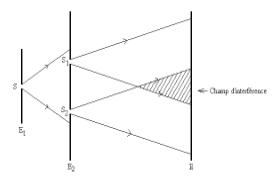
• Observations et interprétation :

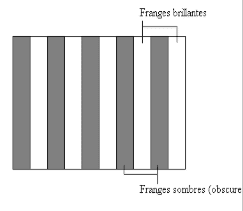
On observe dans le champ d'interférence et parallèlement des raies (lignes) alternativement brillantes et obscures, équidistantes : ce sont des franges d'interférences

• • En un point d'une frange obscure, se superposent deux ondes arrivant en opposition de phase (interférence destructive). Les points d'une frange obscure vibrent avec une amplitude nulle.
  • En un point d'une frange brillante, se superposent deux ondes provenant de $S_1$ er $S_2$ et arrivant en phase (interférences constructives). Les points d'une frange brillante vibrent avec une amplitude maximale.
    
    
• Conclusion : aspect ondulatoire de la lumière

Les interférences lumineuses sont une preuve du caractère ondulatoire de la lumière: Les interférences lumineuses sont une preuve du caractère ondulatoire de la lumière :

$\lambda$ : longueur d'onde.
$C$ : célérité
$T$ : période
$v=\dfrac{1}{T}$ : fréquence
Les longueurs d'onde de la lumière visible dans le vide sont telles que : 

MANQUE FORMULE ?

ou

À une longueur d'onde lumineuse déterminée dans le vide est associée une couleur dite lumière monochromatique.

Conditions d'obtention d'interférences lumineuses

Une expérience d'interférence lumineuse nécessite deux sources cohérentes (synchrones avec un déphasage constant).

NB : les deux sources secondaires $S_1$ et $S_2$, issues d'une source unique $S$ dans le dispositif de Young, sont cohérentes.

Expression de la différence de marche :

Soit $\rm M$ un point de l'écran tel que $\mathrm{HM} = x$

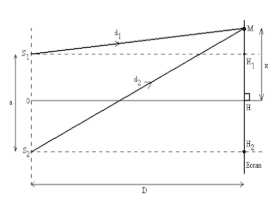
La différence de marche est définie par : $\delta = d_2 - d_1$

Soit le triangle $SM_1H \Rightarrow SM_1^2 = SH^2 + H_1M^2$ $\Leftrightarrow d_1^2 = D^2 + \left(x-\dfrac{a}{2}\right)^2$ (1)

Soit le triangle $S_2H_2 \Rightarrow S_2M^2 = S_2H_2 + H_2M^2$ $\Leftrightarrow d_2^2 = D^2 + \left(x+\dfrac{a}{2}\right)^2$ (2)

(1) et (2) $\Leftrightarrow d_2^2 - d_1^2 = 2ax$ $\Leftrightarrow (d_2 - d_1)(d_2 + d_1) = 2ax$

Approximation : Comme $a$ et $x$ sont très petits devant $D$ ($a$ et $x$ sont de l'ordre du mm tandis que $D$ est de l'ordre du m) $\Leftrightarrow d_1=D$ et $d_2=D \Leftrightarrow d_2 + d_1 = 2D$ $\Leftrightarrow (d_2 - d_1)* 2D = 2ax$ $\Leftrightarrow d_2-d_1 = \dfrac{2ax}{2D}$ $\delta = d_2 - d_1 = \dfrac{ax}{D}$

Expression de l'interfrange $i$

• Positions des franges brillantes : Soit un point $\rm M$ appartenant à une frange brillante, si la différence de marche $\delta$ entre les deux ondes qui parviennent en $\rm M$ est : $\delta = k\lambda$ avec $k\in \mathbb Z$ $\Leftrightarrow \dfrac{ax}{D} = k\lambda \Leftrightarrow x = \frac{k\lambda D}{a}$
• $k = 0 \Leftrightarrow x = 0$ : La frange centrale est toujours une frange brillante.
• Position des franges obscures (sombres) : Un point $\rm M$ appartient à une frange sombre si : $\Leftrightarrow \delta = (2k + \frac{1}{2})\lambda = x$ $\Leftrightarrow \dfrac{ax}{D} = (2k + \dfrac{1}{2})\lambda \Leftrightarrow x = \dfrac{(2k+1)\lambda D}{2a}$ $\delta = (2k + 1)\dfrac{\lambda}{2}$ avec $k \in \mathbb Z$ $x = (k+\dfrac{1}{2})\dfrac{\lambda D}{a}$
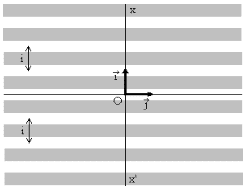
• Expression de l'interfrange $i$ L'interfrange $i$ est la distance entre les milieux de deux franges consécutives de même nature.
  • Soient deux franges brillantes consécutives dont les milieux ont pour abscisse : $x_k = k\dfrac{\lambda D}{a}$ et $x_{k+1} = (k + 1)\dfrac{\lambda D}{a}$
    Par définition : $i = x_{k+1} - x_k = (k + 1)\dfrac{\lambda D}{a} - k\dfrac{\lambda D}{a}$
    $i = \dfrac{\lambda D}{a}$

Ordre d'interférence

L'ordre d'interférence en un point $\rm M$ de l'écran où la différence de marche $\delta$ est définie par $p = \dfrac{\delta}{\lambda}$ où $\lambda$ est la longueur d'onde de la radiation.

Si le point $\rm M$ est le milieu d'une frange brillante, on a alors :

$p = \dfrac{\delta}{\lambda}$ or $\delta = k\lambda \Leftrightarrow p = \dfrac{k\lambda}{\lambda} = k$ : Les franges brillantes ont un ordre d'interférence entier.

Si le point $\rm M$ est le milieu d'une frange sombre, on a alors :

$\displaystyle p = \frac{\delta}{\lambda}$ or $\delta = (2k+1)\dfrac{\lambda}{2} \Leftrightarrow p = \dfrac{(2k+1)\dfrac{\lambda}{2}}{\lambda} = k + \dfrac{1}{2}$ : Les franges sombres ont un ordre d'interférence demi-entier.

2. Interférences en lumière blanche

Spectre de la lumière blanche

La lumiere blanche est formée d'une infinie de radiations allant du rouge au violet et présentant toutes les couleurs de l'arc-en-ciel. L'ensemble de ces radiations (couleurs) constituent le spectre de la lumière blanche. Ces radiations ne sont pas séparées. On dit que le spectre de la lumière blanche est un spectre continu.

Franges en lumière blanche

• Nous observons sur l'écran une frange centrale brillante, blanche. Et de part et d'autre de la frange centrale blanche, quelques franges irisées (colorées) et un peu plus loin l'écran devient uniformément blanchâtre.

• Interprétation
  La lumière blanche étant constituée par un mélange de toutes les radiations visibles allant de (0,4μm) < λ visible < (0,8μm), l'éclairement de l'écran résulte de la superposition des systèmes de franges donnée par chaque lumière monochromatique.
  • Au centre O de l'écran, $S=0$ pour toutes les radiations. Elles présentent donc toutes en o une frange brillante. La superposition de ces franges brillantes de couleurs différentes donne une frange centrale blanche. $i = \dfrac{\lambda D}{a}$ dépend de λ, les systèmes de franges ne coïncident plus. À proximité de O, on voit quelques franges brillantes irisées.
  • Au-delà d'une distance plus grande de la frange centrale, la superposition des diverses franges est tellement complexe que l'oeil ne voit plus que du blanc grisâtre appelé blanc d'ordre supérieur. Lorsqu'on analyse ce blanc au spectroscope, on voit des bandes noires qui correspondent aux radiations manquantes et que l'on désigne sous le nom de cannelures : on parle pour cette raison de spectre cannelé.

Remarque : Les radiations manquantes en un point donné sont celles qui y présentent une frange obscure donc celles pour lesquelles au point considéré $S=(2K+1) \dfrac{\lambda}{2}$.

Conclusion : Le phénomène d'interférences lumineuses n'est pas seulement une preuve du caractère ondulatoire de la lumière, mais c'est aussi une méthode de mesure physique de longueur d'onde d'une source monochromatique.