1. Induction magnétique :
Flux magnétique
Lorsque les lignes de champ d’un champ magnétique traverse la surface plane d’un circuit plan : On dit qu’il est traverse par flux magnétique :
- Expression du flux : $\Phi = B\times S\times cos\theta$ avec $\theta = \left(\overrightarrow{B},\overrightarrow{S}\right)$
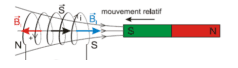
- $\theta = 0$ $\Rightarrow\Phi = B.S$ ;
- $\displaystyle 0\lt\theta\lt\frac{\pi}{2}$ $\Rightarrow$ $\Phi \gt 0$ ;
- $\displaystyle \theta = \frac{\pi}{2}$ $\Rightarrow$ $\Phi = 0$ ;
- $\theta = \pi$ $\Rightarrow$ $\Phi = - B.S$ ;
- $\displaystyle \frac{\pi}{2}\lt\theta\lt\pi$ $\Rightarrow$ $\Phi \lt 0$
NB : Le flux s’exprime en weber (wb).
Phénomène d’Induction magnétique
Lorsque le flux magnétique traversant la surface plane d’un circuit fermé varie (il y a variation de flux), il y a naissance d’un courant de faible intensité appelé courant induit : c’est le phénomène d’induction magnétique.
Le déplacement de l’aimant crée une variation de flux qui induit une force électromotrice induite qui fait circuler un courant Induit $i$ dans le circuit.
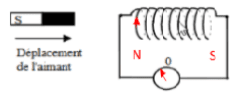
NB : L’aimant est l’inducteur et la bobine est l’induit.
f.é.m. induite :
Toute variation de flux magnétique à travers un circuit plan crée une f.é.m. induite d’expression : $e = \displaystyle -\frac{d\Phi}{dt}$
Loi de Lenz : sens du courant induit
Le sens du courant induit est tel que par ses effets, il s’oppose à la cause qui lui donne naissance.
2. Auto-induction magnétique
Lorsque le phénomène d’induction magnétique se passe dans une bobine, la bobine est à la fois l’inducteur et l’induit : On parle d’auto-induction magnétique dans une bobine.
Flux propre d’une bobine
$\Phi_p = NBS = N \times \mu_0 \times \dfrac{N}{l} \times S\times i = \mu_0 \times \dfrac{N^2}{l} \times S\times i$
Inductance de la bobine
$\Phi_p = Li \Rightarrow L = \mu_0\times\dfrac{N^2}{l} \times S$
- $N$ = nombre total de spores de la bobine
- $S$ = surface d’une spire (en m²)
- $l$ = longueur de la bobine (en m)
- $\mu_0 = 4\pi.10^{-7}$ (SI) perméabilité du vide
NB : L’inductance s’exprime en henry (H)
f.é.m. d’auto-induction
$\displaystyle e= -\frac{d\Phi_p}{dt} = -L\frac{di}{dt}$
Expression de la tension aux bornes de la bobine :
- En convention générateur : $\displaystyle U= e-ri = -L\frac{di}{dt}-ri$
- En convention récepteur : $\displaystyle U = e +ri = L\frac{di}{dt} + ri$
Étude du dipôle (R, L) : établissement et annulation du courant
Un générateur basse fréquence applique une tension créneau aux bornes d’une bobine (L, r) en série avec un résistor de résistance R. (voir figure ci-dessous) :
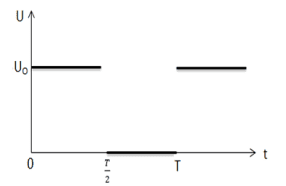
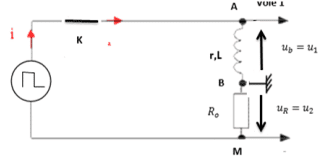
- Sur [0 ; +∞[ : établissement du courant :
- Équation différentielle vérifiée par i : $\displaystyle \frac{di}{dt}+\frac{R+r}{L}i = \frac{U_0}{L}$
- Solution de l’équation différentielle : $i = I_0 \left(1 - e^{-\frac{t}{\tau}}\right)$ avec $\displaystyle I_0 = \frac{U_0}{R+r}$ et $\displaystyle ;\tau = \frac{L}{R+r}$
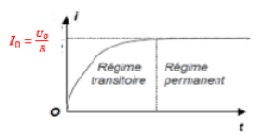
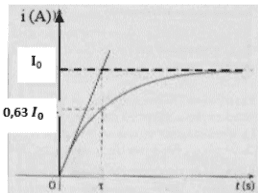
- Détermination graphique de $\tau$ (constante de temps du dipôle (R, L) :
- A t=$\tau$ On a i = 63% $I_0$
- La tangente a la courbe a t = 0 la droite i=$I_0$ au Point t =$\tau$
- Sur $[0~;\dfrac{T}{2}[$ : annulation du courant :
-
- Équation différentielle vérifiée par $i$ : $\displaystyle \frac{di}{dt}+\frac{R+r}{L}i = 0$
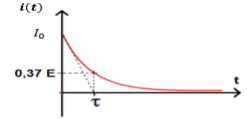
- Solution de l’équation différentielle : $\displaystyle i = I_0\times \rm e^{-\frac{t}{\tau}}$
- Détermination graphique de $\tau$ :
- À $t = \tau$ On a $i = 37 \%I_0$$